Գաղափար հատույթի մասին — դաս։ Երկրաչափություն, 10-րդ դասարան.

Գաղափար հատույթի մասին

Բազմանիստի հատման հարթություն կարելի է անվանել ցանկացած հարթություն, որի երկու կողմերում կան բազմանիստի կետեր:

Հատման հարթությունը բազմանիստի նիստերը հատում է հատվածներով:

Բազմանկյունը, որի կողմերը այդ հատվածներն են, կոչվում է բազմանիստի հատույթ:

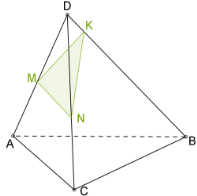
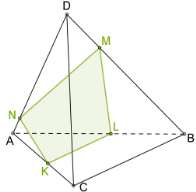
Քանի որ քառանիստ ունի \(4\) նիստ, ապա նրա հատույթը կարող է լինել եռանկյուն կամ քառանկյուն (տես ներքևի նկարները):

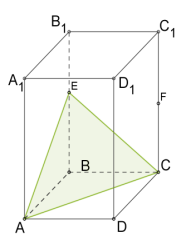
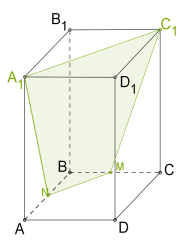
Քանի որ զուգահեռանիստ ունի \(6\) նիստ, ապա նրա հատույթը կարող է լինել եռանկյուն, քառանկյուն, հնգանկյուն կամ վեցանկյուն (տես ներքևի նկարները):

Հատույթը կառուցելիս պետք է հիշել որոշ գիտելիքներ անցած թեմաներից:

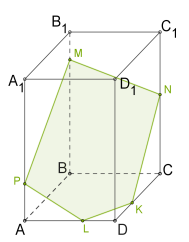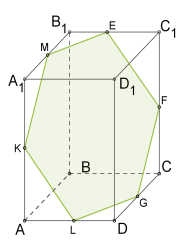1.Եթե երկու կետեր պատկանում են հարթությանը, ապա նրանցով անցնող ուղիղը ևս պատմանում է այդ հարթությանը:

2. Եթե երկու հարթություններ ունեն ընդհանուր կետ, ապա նրանք հատվում են ընդհանուր ուղիղով:

3. Եթե երկու զուգահեռ հարթություններ հատվում են երրորդ հարթությամբ, ապա հատման ուղիղները ևս զուգահեռ են:

Օրինակ

Կառուցենք զուգահեռանիստի հատույթ, որն անցնում է \(K\), \(M\) և \(N\) կետերով:

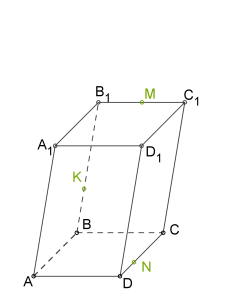
1. Տանենք \(MK\) հատվածը, քանի որ երկու կետերն էլ գտնվում են հատույթի մեջ:

MK \cap {CC}_{1} = X

, քանի որ նույն հարթության մեջ գտնվող ոչ զուգահեռ ուղիղները հատվում են:

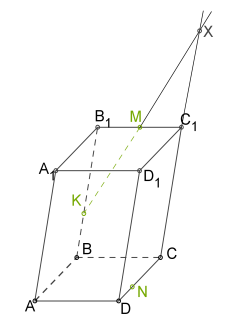
3. Տանենք \(XN\) հատվածը, քանի որ երկու կետերն էլ գտնվում են հատույթի մեջ:

XN \cap D_{1} C_{1} = P

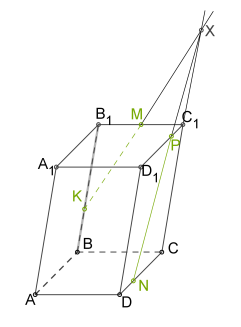
5. Տանենք \(MP\) հատվածը, քանի որ երկու կետերն էլ գտնվում են հատույթի մեջ:

6. Զուգահեռանիստի ներքևի հիմքում \(N\) կետով տանենք

NL ∥ MP

ուղիղներ (եթե երկու զուգահեռ հարթություններ հատվում են երրորդ հարթությամբ, ապա հատման ուղիղները զուգահեռ են):

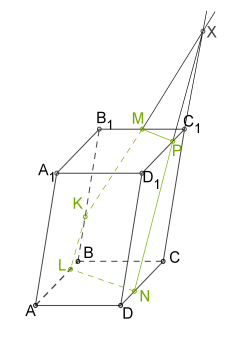
7. Միացնելով \(N\) և \(L\) կետերը, ստանում ենք \(MPNLK\) հատույթը:

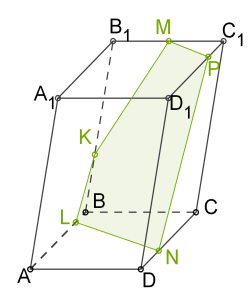
Աղբյուրները

Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009

Սխա՞լ ես գտել

1. Գաղափար հատույթի մասին