1. Եռանկյունների հավասարության առաջին հայտանիշը

 

Մենք արդեն գիտենք, որ երկու պատկերներ, այդ թվում՝ երկու եռանկյուններ կոչվում են հավասար, եթե վերադրումով դրանք կարող են համընկնել:

 

 

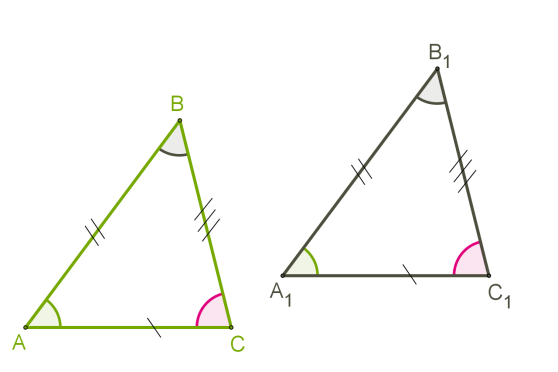
Ընդ որում, համընկնում են բոլոր կողմերը և բոլոր անկյունները:

 

Գործնականում միշտ չէ, որ պատկերների համեմատման համար հաջողվում է վերադրել դրանք: Հաճախ պետք է լինում բավարարվել մի քանի չափումներով և դրանց հիման վրա եզրակացություն կատարել պատկերների հավասարության վերաբերյալ:

Ապացուցենք, որ երկու եռանկյունների հավասարության համար բավական է, որ հավասար լինեն եռանկյունների որևէ երկու կողմեր և նրանցով կազմված անկյունները:

 

 

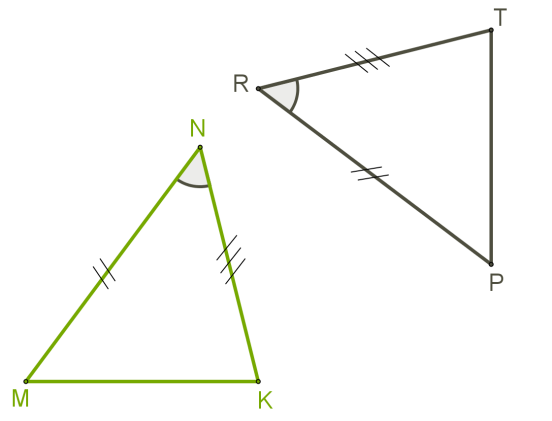
Համոզվենք, որ այս պայմանների դեպքում եռանկյունները կարելի է վերադրել այնպես, որ դրանք համընկնեն:

1. Քանի որ$\measuredangle N=\measuredangle R$, ապա $\mathrm{\Delta }\mathit{MNK}$ եռանկյունը կարելի է վերադրել $\mathrm{\Delta }\mathit{PRT}$ եռանկյան վրա այնպես, որ \(N\) գագաթը համընկնի \(R\) գագաթին, իսկ \(NM\) և \(NK\) կողմերն ընկնեն համապատասխանաբար \(RP\) և \(RT\) ճառագայթների վրա:

 

2. Քանի որ $\mathit{MN}=\mathit{PR},\mathit{KN}=\mathit{TR}$, ապա \(MN\) կողմը կհամընկնի \(PR\) կողմին, իսկ \(KN\) կողմը՝ \(TR\) կողմին, մասնավորապես, կհամընկնեն \(M\) և \(P\), \(K\) և \(T\) կետերը:

 

3. Հետևաբար, կհամընկնեն \(MK\) և \(PT\) կողմերը: Այսպիսով, $\mathrm{\Delta }\mathit{MNK}$ և $\mathrm{\Delta }\mathit{PRT}$ եռանկյուններն ամբողջովին կհամընկնեն՝ հետևաբար, դրանք հավասար են: