Զուգահեռ ուղիղների սահմանումը և հարթության վրա դրանց հատկությունների ապացուցումը

Հարթության վրա երկու ուղիղներ կա՛մ ունեն ընդամենը մեկ ընդհանուր կետ, կա՛մ չունեն ոչ մի ընդհանուր կետ:
Առաջին դեպքում ասում են, որ ուղիղները հատվում են, իսկ երկրորդ դեպքում՝ չեն հատվում:
Հարթության վրա գտնվող \(a\) և \(b\) ուղիղները կոչվում են զուգահեռ, եթե նրանք չեն հատվում: Այդ հանգամանքը նշանակում են այսպես՝ :
Ուշադրություն
Եթե ուղիղները նույն հարթության մեջ չեն, ապա կարող է ստացվել այնպես, որ ուղիղները չեն հատվում, բայց զուգահեռ էլ չեն:

Հարթության վրա գտնվող ուղիղների զուգահեռության հայտանիշներից մեկն ասում է հետևյալը.
1. Եթե հարթության վրա գտնվող երկու ուղիղներ ուղղահայաց են նույն ուղղին, ապա դրանք զուգահեռ են:
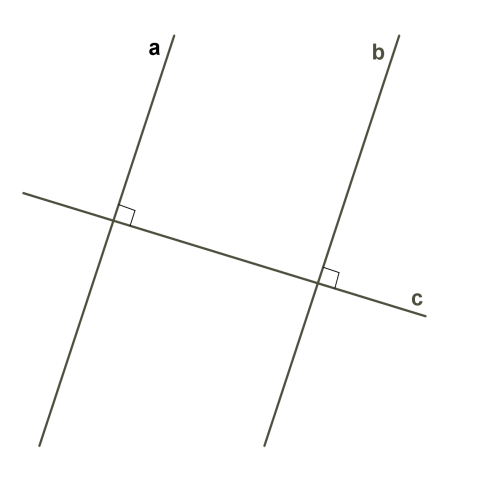
Այս հայտանիշը հեշտ է ապացուցել, եթե հիշենք, որ հարթության վրա ցանկացած կետից տրված ուղղին կարելի է տանել միայն մեկ ուղղահայաց:
Ենթադրենք, թե նույն ուղղին ուղղահայաց ուղիղները զուգահեռ չեն, այսինքն՝ ունեն ընդհանուր կետ:
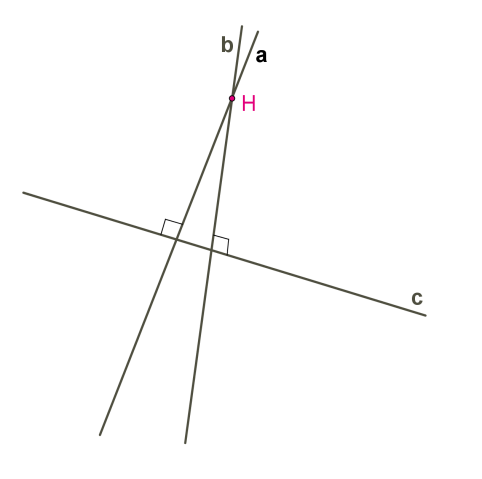
Ստացվում է հակասություն՝ մեկ \(H\) կետից \(c\) ուղղին տարված են երկու ուղղահայացներ: Այդպիսի բան հնարավոր չէ, ուստի նույն ուղղին ուղղահայաց երկու ուղիղները զուգահեռ են:
Այլ հայտանիշներ ստանալու համար ծանոթանանք անկյունների որոշ տեսակների հետ
1) Հիշենք, որ մեզ հայտնի են հատվող ուղիղների կազմած անկյունների անվանումներն ու հատկությունները:
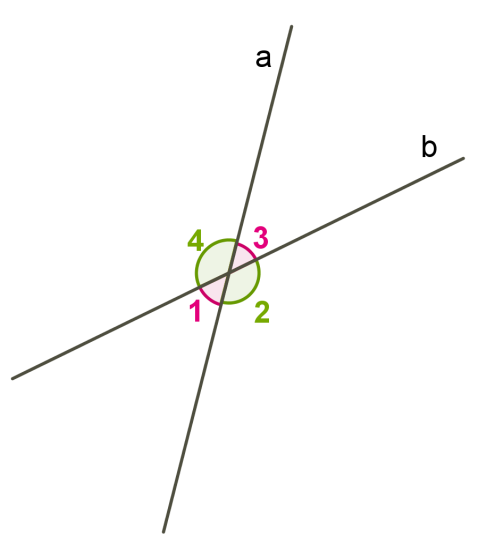
Հակադիր անկյունները հավասար են՝
Կից անկյունների գումարը է՝
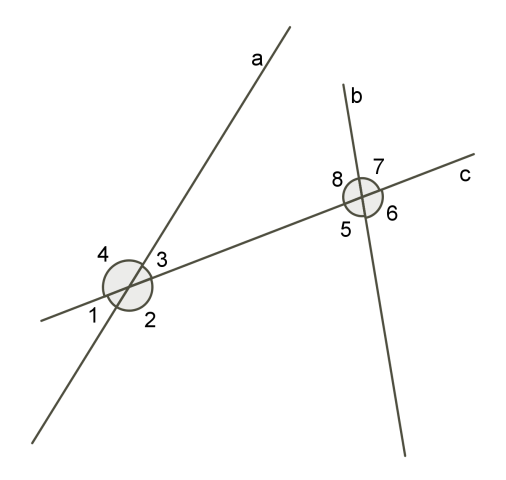
Խաչադիր անկյուններ՝
Համապատասխան անկյուններ՝
Միակողմանի անկյուններ՝
Այս անկյունները կօգնեն ձևակերպել \(a\) և \(b\) ուղիղների զուգահեռությունը: Այսպիսով, հարթության մեջ ուղիղների զուգահեռության մյուս հայտանիշն ասում է հետևյալը.
2. Եթե երկու ուղիղներ հատվում են երրորդով, և խաչադիր կամ համապատասխան անկյունները հավասար են, կամ միակողմանի անկյունների գումարը հավասար է \(180°\)-ի, ապա ուղիղները զուգահեռ են:
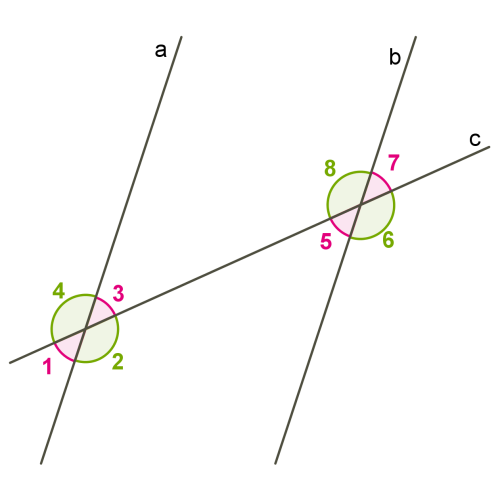
Սրանք, ըստ էության, երեք առանձին հայտանիշներ են, բայց մենք դրանք միավորեցինք մեկ հայտանիշի մեջ:
Ապացուցենք այս հայտանիշը.
Սկզբում ապացուցենք, որ եթե \(a\) և \(b\) ուղիղները հատվում են \(c\) ուղղով, և խաչադիր անկյունները հավասար են, ապա \(a\) և \(b\) ուղիղները զուգահեռ են:
Օրինակ, եթե, ապա
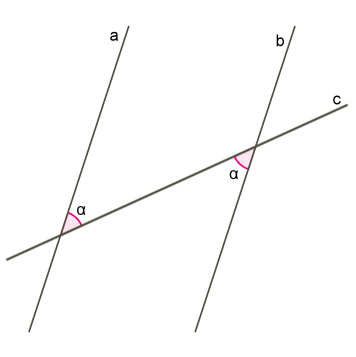
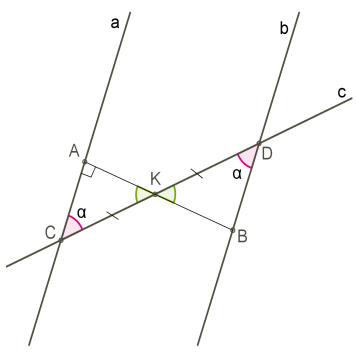
\(1\)) \(C\)-ով և \(D\)-ով նշանակենք այն կետերը, որոնցում \(a\) և \(b\) ուղիղները հատվում են \(c\) ուղղի կողմից: Այդ հատվածի \(K\) միջնակետով տանենք \(AB\) ուղղահայացը \(a\) ուղղին:
\(2\))\(=\), որպես հակադիր անկյուններ,\(=\)\(=\), \(CK = KD\)՝ հետևաբար՝ \(=\), ըստ եռանկյունների հավասարության երկրորդ հայտանիշի:
\(3\)) Ակնհայտ է, որ եթե ուղղանկյուն եռանկյուն է, ապա ուղղանկյուն է նաև եռանկյունը, և \(AB\)-ն ուղղահայաց է \(b\) ուղղին:
\(4\)) Համաձայն առաջին հայտանիշի, եթե ուղիղները ուղղահայաց են նույն ուղղին, ապա նրանք զուգահեռ են:
\(5\)) Այն դեպքում, երբ հավասար են համապատասխան անկյունները, նկատի ենք ունենում, որ հակադիր անկյունները հավասար են, և ապացույցը տանում ենք նույն \(1-4\) քայլերով:
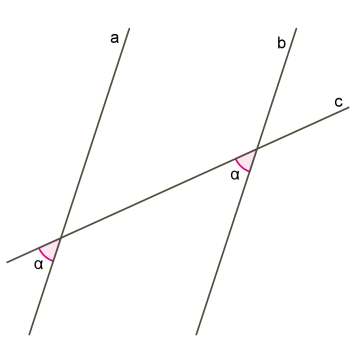
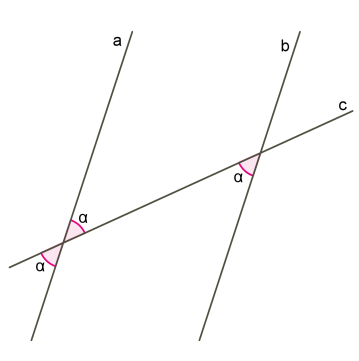
\(6\)) Այն դեպքում, երբ միակողմանի անկյունների գումարը հավասար է \(180°\)-ի, նկատի ենք ունենում, որ կից անկյունների գումարը ևս հավասար է \(180°\)-ի և ապացույցը շարունակում ենք \(1 - 4\) կետերով:
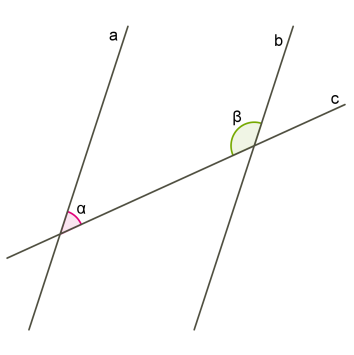
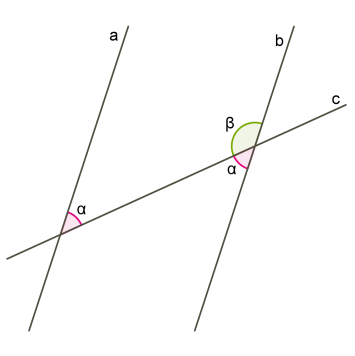


3. Ապացուցված հայտանիշը կարելի է ձևակերպել որպես զուգահեռ ուղիղների հատկություն:
Երկու զուգահեռ ուղիղները երրորդ ուղղով հատվելիս.
- խաչադիր անկյունները հավասար են,
- համապատասխան անկյունները հավասար են,
- միակողմանի անկյունների գումարը հավասար է \(180°\)-ի:
Զուգահեռ ուղիղների մյուս հատկությունները կդիտարկենք հաջորդ պարագրաֆի տեսության մեջ:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011:


