Ուռուցիկ բազմանկյուն — դաս։ Երկրաչափություն, 8-րդ դասարան.

Ուռուցիկ բազմանկյուններ

Բազմանկյունը, որի բոլոր անկյունները

180 °

-ից փոքր են, կոչվում է ուռուցիկ բազմանկյուն:

Ներքևի \(ABCDE\) հնգանկյունը ուռուցիկ է:

Ուռուցիկ \(n\)-անկյան անկյունների գումարը

Ընդհանուր դեպքում, բազմանկյունը կարելի անվանել \(n\)-անկյուն, եթե այն ունի \(n\) հատ կողմ, \(n\) հատ անկյուն և \(n\) հատ գագաթ:

Ուռուցիկ \(n\)-անկյան անկյունների գումարը հավասար է

180^{°} \cdot (n - 2)

-ի:

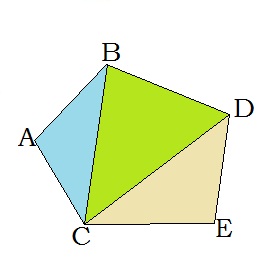
Figūra 3.jpg

Ցանկացած բազմանկյուն կարելի է բաժանել եռանկյունների: Այդպես է արված վերևի նկարում: Եռանկյունների թիվը \(2\) -ով քիչ է բազմանկյան կողմերի թվից: Եռանկյունների կողմերը բազմանկյան կողմեր և անկյունագծեր են:

Ցանկացած եռանկյան ներքին անկյունների գումարը

180 °

է: Հետևաբար, ուռուցիկ \(n\)-անկյան անկյունների գումարը

180^{°} \cdot (n - 2)

է:

Օրինակ

Հաշվենք ներքևի տասնմեկանկյան անկյունների գումարը:

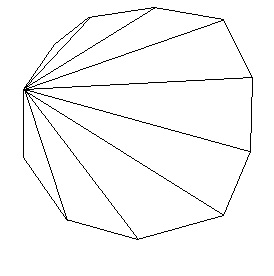
Նկարը կարելի էր նույնիսկ չգծել, այլ օգտվել բանաձևից:

Կիրառելով բանաձևը, ստանում ենք՝

180^{°} \cdot (n - 2) = 180^{°} \cdot (11 - 2) = 180^{°} \cdot 9 = 1620^{°}

Կանոնավոր բազմանկյուններ

Այն ուռուցիկ բազմանկյունը, որի բոլոր կողմերը և անկյունները հավասար են, կոչվում է կանոնավոր բազմանկյուն:

Կանոնավոր եռանկյունը հավասարակողմ եռանկյունն է:

Կանոնավոր քառանկյունը քառակուսին է:

Քառանկյուններ

Բազմանկյունը կոչվում է քառանկյուն, եթե այն ունի \(4\) կողմ:

Քառանկյունն ունի \(4\) կողմ, \(4\) գագաթ, \(4\) անկյուն, \(2\) անկյունագիծ: Քառանկյան ոչ կից կողմերը կոչվում են հանդիպակաց:

Ուռուցիկ բազմանկյան անկյունների գումարի բանաձևի մեջ \(n\)-ի փոխարեն \(4\) տեղադրելով, ստանում ենք հետևյալ պնդումը:

Ուռուցիկ քառանկյան անկյունների գումարը հավասար է

360^{°}

-ի:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2007:

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ