Էլիպս
Դիտարկենք այս շրջանագիծը:
Եթե պատկերացնենք, որ շրջանագիծը սեղմվում է տրամագծի նկատմամբ, ապա կստացվի մի պատկեր, որն անվանում են էլիպս:
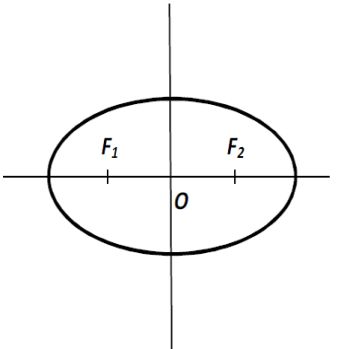
Պարզվում է, որ էլիպսն ունի երկու կարևոր կետեր (կիզակետեր), որոնցից կախված է էլիպսի տեսքը:
Էլիպս կոչվում է երկրաչափական այն պատկերը, որը կազմված է հարթության բոլոր այն կետերից, որոնց համար հաստատուն է մնում նրանց հեռավորությունների գումարը տրված երկու կետերից: Տրված կետերը (վերևի նկարի և կետերը) կոչվում են էլիպսի կիզակետեր (ֆոկուսներ):
Էլիպսի համաչափության հատկությունները
Էլիպսի սահմանումից բխում են հետևյալ երեք հատկությունները:
1) և կետերով անցնող ուղիղը էլիպսի համաչափության առանցքն է:
2) և ծայրակետերով հատվածի միջնուղղահայացը էլիպսի համաչափության առանցքն է:
3) Այդ երկու ուղիղների հատման կետը էլիպսի համաչափության կենտրոնն է:
կետը կոչվում է էլիպսի կենտրոն:
Եթե էլիպսի գծագիրը տեղադրենք սկզբնակետով և նշված համաչափության առանցքներով կոորդինատային հարթության վրա, ապա ձևակերպված հատկությունները նշանակում են, որ.
Ուշադրություն
երկու կոորդինատային առանցքները էլիպսի համար համաչափության առանցքներ են, իսկ կոորդինատների սկզբնակետը՝ էլիպսի համաչափության կենտրոնն է:
Էլիպսը հանդիպում է բազմաթիվ իրավիճակներում:
Ավտոմեքենայի լապտերների արձակած լույսն ունի էլիպսի տեսք:
Հայտնի է, որ Երկիր մոլորակը ձվաձև է՝ այն սեղմված է հասարակածի նկատմամբ մոտավորապես կիլոմետրով:
Մոլորակները Արեգակի շուրջ պտտվում են էլիպսաձև ուղեծրերով, ընդ որում՝ Արեգակը գտնվում է այդ էլիպսի կիզակետերից մեկում:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև,, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:


