Եռանկյունաչափական հիմնական բանաձևը

Դիտարկենք միավոր շրջանագծում տրված \(AOX\) եռանկյունը:

Անկյուններից մեկը նշանակենք

α

-ով:

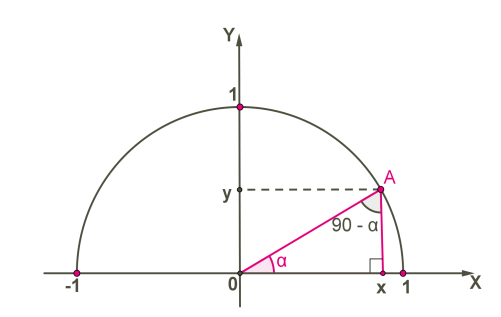
\(AOX\) եռանկյան մեջ կիրառենք Պյութագորասի թեորեմը:

Ստանում ենք՝

{AX}^{2} + {OX}^{2} = 1

Քանի որ

\sin α = \frac{AX}{AO}; \cos α = \frac{OX}{AO}

, և նկատի ունենալով, որ միավոր շրջանագծի շառավիղը հավասար է մեկի՝

\(AO = 1\), ստանում ենք՝

\sin^{2} α + \cos^{2} α = 1

\sin^{2} α + \cos^{2} α = 1

հավասարությունը կոչվում է եռանկյունաչափական հիմնական նույնություն:

Այս հավասարությունը թույլ է տալիս հաշվել անկյան սինուսը, եթե հայտնի է այդ անկյան կոսինուսը՝

\begin{array}{l} \sin^{2} α + \cos^{2} α = 1 \\ \sin^{2} α = 1 - \cos^{2} α \\ \sin α = \sqrt{1 - \cos^{2} α} \end{array}

կամ հաշվել անկյան կոսինուսը, եթե հայտնի է այդ անկյան սինուսը՝

\begin{array}{l} \sin^{2} α + \cos^{2} α = 1 \\ \cos^{2} α = 1 - \sin^{2} α \\ \cos α = \pm \sqrt{1 - \sin^{2} α} \end{array}

Սուր անկյունների դեպքում պետք է վերցնել «\(+\)» նշանը, իսկ բութ անկյունների դեպքում՝ «\(-\)» նշանը:

Եթե

\sin^{2} α + \cos^{2} α = 1

հիմնական նույնության երկու մասերը բաժանենք

\cos^{2} α

վրա, ապա կստանանք անկյան տանգենսը կոսինուսի հետ կապող հետևյալ բանաձևը՝

\begin{array}{l} \frac{\sin^{2} α}{\cos^{2} α} + 1 = \frac{1}{\cos^{2} α} \\ {tg}^{2} α + 1 = \frac{1}{\cos^{2} α} \end{array}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, "Զանգակ", 2013

Սխա՞լ ես գտել

1. Եռանկյունաչափական հիմնական բանաձևը