Կետի կոորդինատները
Դիցուք կոորդինատային հարթության վրա տրված է \(A(x;y)\) կետը:
\(A\) կետի \(AO\) հեռավորությունը կոորդինատների \(O\) սկզբնակետից նշանակենք \(R\)-ով և տանենք \(O\) կենտրոնով և \(R\) շառավղով շրջանագիծը:
Այդ շրջանագիծը անցնում է \(A\) կետով:
\(AO\) հատվածի և աբսցիսների դրական կիսաառանցքի կազմած անկյունը նշանակենք -ով:
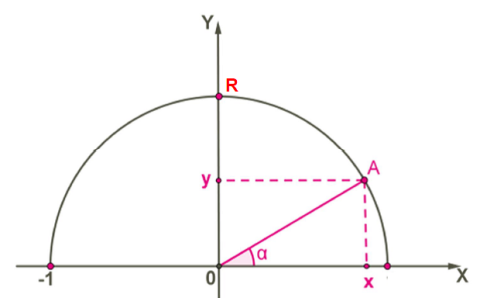
\(A(x;y)\) կետի \(x = OX\) և \(y = OY\) կոորդինատները արտահայտենք \(AO\) հատվածի \( R\) երկարության և անկյան միջոցով:
Դիտարկենք սուր անկյունով \(AOX\) ուղղանկյուն եռանկյունը:
Գիտենք, որ սուր անկյան սինուսը հավասար է անկյան դիմացի էջի հարաբերությանը ներքնաձիգին, իսկ կոսինուսը՝ կից էջի հարաբերությանը ներքնաձիգին:
Այսպիսով՝
Այստեղից ստանում ենք՝
Քանի որ \(x = OX\), և \(y = OY = AX\) թվերը \(A(x;y)\) կետի կոորդինատներն են, և \(AO = R\), ապա՝
Կոորդինատային հարթության վրայի \(A\) կետի կոորդինատները գտնելու համար պետք այդ կետը միացնել կոորդինատների \(O\) սկզբնակետի հետ, գտնել \(OA\) հատվածի \(OA = R\) երկարությունը և \(OA\) հատվածի և աբսցիսների դրական կիսաառանցքի կազմած անկյունը:
Այդ դեպքում \(A\) կետի կոորդինատներն են՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013


