Եռանկյան մակերեսի և արտագծյալ շրջանագծի շառավղի միջև կապը

Եռանկյան մակերեսի և արտագծյալ շրջանագծի շառավղի կապը

Դիցուք ունենք \(a\), \(b\), \(c\) կողմերով \(ABC\) եռանկյունը:

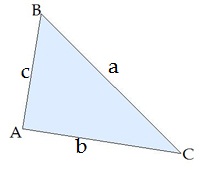
Ըստ եռանկյան մակերեսի մասին թեորեմի՝

S_{ABC} = \frac{ab \cdot \sin C}{2}

Մյուս կողմից, գիտենք, որ

\frac{c}{sinC} = 2 R

, որտեղ \(R\)-ը եռանկյան արտագծյալ շրջանագծի շառավիղն է: Այստեղից ստանում ենք՝

\sin C = \frac{c}{2 R}

Տեղադրելով մակերեսի բանաձևի մեջ, ստանում ենք՝

S_{ABC} = \frac{ab}{2} \cdot \frac{c}{2 R} = \frac{abc}{4 R}

Այսպիսով, ապացուցեցինք հետևյալ թեորեմը:

Եռանկյան մակերեսը հավասար է նրա կողմերի արտադրյալի և արտագծյալ շրջանագծի շառավղի քառապատիկի հարաբերությանը՝

S_{ABC} = \frac{abc}{4 R}

Ապացուցված բանաձևը թույլ է տալիս գտնել տրված կողմերով եռանկյան արտագծյալ շրջանագծի շառավիղը:

Օրինակ

Խնդիր: Դիցուք տրված \(a = 4\), \(b = 7\), \(c = 9\) կողմերով \(ABC\) եռանկյունը:

Պետք է գտնել \(ABC\) եռանկյան արտագծյալ շրջանագծի շառավիղը:

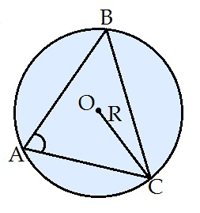
Լուծում: Հերոնի բանաձևի միջոցով գտնենք \(ABC\) եռանկյան մակերեսը՝

S_{ABC} = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{10 \cdot 6 \cdot 3 \cdot 1} = 6 \sqrt{5}

Օգտվելով ապացուցված բանաձևից, ստանում ենք արտագծյալ շրջանագծի շառավիղը՝

R = \frac{abc}{4 S} = \frac{4 \cdot 7 \cdot 9}{6 \sqrt{5}} = 8.4 \sqrt{5}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ» 2013

Սխա՞լ ես գտել

1. Եռանկյան մակերեսի և արտագծյալ շրջանագծի շառավղի միջև կապը