Ուղիղ պրիզմայի ծավալը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Ուղիղ պրիզմայի ծավալը

Ուղիղ պրիզմայի ծավալը հավասար է հիմքի մակերեսի և բարձրության արտադրյալին՝

V = S_{հիմք} \cdot H

Համոզվենք դրանում մի քանի քայլերով:

1. Դիտարկենք ուղղանկյունանիստ, որի անկյունագծերով տարված է հատույթ:

Հատույթով ուղղանկյունանիստը տրոհվում է երկու հավասար եռանկյուն պրիզմաների, որոնց հիմքերում հավասար ուղղանկյուն եռանկյուններ են:

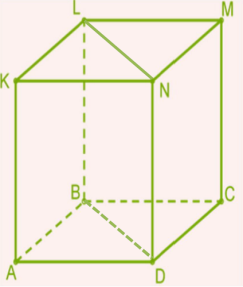
Ուղղանկյունանիստի ծավալի բանաձևից ստանում ենք՝

\begin{array}{l} V_{ուղղ} = 2 \cdot V_{պրիզմա} \\ S_{ABCD} \cdot H = 2 \cdot V_{\begin{array}{l} պրիզմա \end{array}} \\ V_{պրիզմա} = \frac{S_{ABCD} \cdot H}{2} = S_{ABD} \cdot H \end{array}

Այսպիսով,

V = S_{հիմք} \cdot H

բանաձևը ճիշտ է այն դեպքում, երբ պրիզմայի հիմքում ուղղանկյուն եռանկյուն է:

2. Եթե պրիզմայի հիմքում կամայական եռանկյուն է, ապա տանելով հարթություն նրա հիմքերի բարձրություններով, ստանում ենք երկու պրիզմաներ, որոնց հիմքերում ուղղանկյուն եռանկյուններ են, և այս դեպքը բերվում է դիտարկված դեպքին՝ նկարում (պրիզմայի հիմքն է):

Այսպիսով,

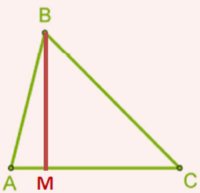
V = S_{հիմք} \cdot H

բանաձևը ճիշտ է, կամայական ուղիղ եռանկյուն պրիզմայի դեպքում:

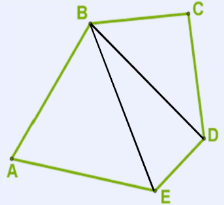
3. Վերջապես, ընդհանուր դեպքը, երբ ուղիղ պրիզմայի հիմքում կամայական բազմանկյուն է՝ բերվում է մի քանի եռանկյուն պրիզմաների դեպքին, եթե տանել հարթություններ հիմքերի բազմանկյունների նույն գագաթից դուրս եկող անկյունագծերով:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ», 2013

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Ուղիղ պրիզմայի ծավալը

Տեսություն