1. Մարմնի իմպուլս:Իմպուլսի պահպանման օրենքը: Ռեակտիվ շարժում

Մարմնի իմպուլս

Շարժվող մարմնի գործողությունը կախված է նրա զանգվածից և արագությունից:

Օրինակ

մեծ արագությամբ շարժվող գնդակը ֆուտբոլիստը կարող է կանգնեցնել ոտքով կամ գլխով (տե՛ս նկար 1), բայց մարդը չի կարող կանգնեցնել նույնիսկ շատ փոքր արագությամբ շարժվող գնացքը (տե՛ս նկար 2): Թենիսի գնդակը, դիպչելով մարդուն, վնաս չի տալիս, սակայն ավելի փոքր զանգվածով, բայց մեծ արագությամբ շարժվող ատրճանակից դուրս թռած գնդակը կարող է մեծ վնաս հասցնել մարդուն:

Այն ֆիզիկական մեծությունը, որը հավասար է մարմնի զանգվածի և արագության արտադրյալին, կոչվում է մարմնի շարժման քանակ կամ իմպուլս (լատիներեն «impulsus»` հրում, հարված բառերից):

Մարմնի իմպուլսը սովորաբար նշանակում են $p$ տառով՝ $P = mv$

Քանի որ արագությունը վեկտորական մեծություն է, իսկ զանգվածը՝ սկալյար, ապա իմպուլսը վեկտորական մեծություն է: Իմպուլսի ուղղությունը համընկնում է արագության ուղղության հետ, իսկ նրա բանաձևը ներկայացվում է հետևյալ տեսքով՝

\vec{p} = m \vec{v}

Ուշադրություն

Իմպուլսի սահմանումից բխում է, որ նրա չափման միավորը ՄՀ-ում $1$ կգ·մ/վ-ն է: Դա $1$ մ/վ արագությամբ շարժվող $1$ կգ զանգվածով մարմնի իմպուլսն է:

Մարմինների համակարգի իմպուլսը

Մարմինների համակարգի իմպուլս կոչվում է այդ համակարգը կազմող մարմինների իմպուլսների գումարը:
Համակարգի իմպուլսը հաշվելիս պետք է հիշել, որ համակարգը կազմող մարմինների իմպուլսները վեկտորներ են: Նրանց գումարը նույնպես վեկտոր է, ուստի համակարգի իմպուլսը վեկտորական մեծություն է:

Ուրեմն համակարգն ունի ուղղություն և մեծություն:

Իմպուլսի պահպանման օրենքը փակ համակարգերում

Մարմինների փակ համակարգ կոչվում է միայն միմյանց հետ փոխազդող մարմիններից կազմված համակարգը:

Համակարգի մարմինների միջև փոխազդեցության ուժերն ընդունված է անվանել ներքին ուժեր: Իսկ համակարգի մարմինների վրա այլ մարմինների (որոնք չեն մտնում համակարգի մեջ) կողմից ազդող ուժերն անվանում են արտաքին ուժեր: Շատ դեպքերում փակ են համարում նաև այն համակարգը, որը կազմող մարմինների վրա ազդող արտաքին ուժերի համազորը զրո է, այսինքն՝ համակարգի վրա արտաքին ազդեցությունները համակշռված են:

Փակ համակարգ կազմող մարմինների իմպուլսների գումարը մնում է անփոփոխ:

Նյուտոնի երկրորդ օրենքի առավել ընդհանուր ձևակերպումը

Ըստ Նյուտոնի երկրորդ օրենքի՝ ուժի ազդեցության հետևանքով $m$ զանգվածով մարմնի ձեռք բերած արագացումը՝ $\vec{a} = \frac{\vec{F}}{m}$

հայտնի է, որ $\vec{a} = \frac{Δ \vec{v}}{t}, հետևաբար \frac{Δ \vec{v}}{t} = \frac{F}{m}, որտեղից m Δ \vec{v} = \vec{F} t, կամ Δ \vec{p} = \vec{F} t$

Վերջին հավասարության ձախ մասում մարմնի իմպուլսի

Δ \vec{p}

փոփոխությունն է $t $ ժամանակամիջոցում, իսկ աջ մասում՝ ուժի և նրա ազդման տևողության արտադրյալը, որը նույնպես հատուկ անուն ունի՝ ուժի իմպուլս:

Ստացված հավասարումը Նյուտոնի $երկրորդ$ օրենքի առավել ընդհանուր ձևակերպումն է: Նյուտոնը հենց այսպես է ձևակերպել իր $երկրորդ$ օրենքը.

Մարմնի իմպուլսի փոփոխությունը հավասար է նրա վրա ազդող ուժի իմպուլսին:

Նյուտոնի $երկրորդ$ օրենքի այս ձևակերպումը վերաբերում է առանձին վերցրած մարմնին: Մի քանի մարմիններից կազմված համակարգի համար Նյուտոնի $երկրորդ$ օրենքը ձևակերպվում է այսպես.

Մարմինների համակարգի իմպուլսի փոփոխությունը հավասար է այդ համակարգի մարմինների վրա ազդող արտաքին ուժերի համազորի իմպուլսին:

Մարմինների համակարգի համար Նյուտոնի երկրորդ օրենքը նույնպես ներկայացվում է նույն հավասարման տեսքով: Այս դեպքում

Δ \vec{p}

–ն համակարգը կազմող մարմինների իմպուլսների փոփոխությունների գումարն է, իսկ

\vec{F}

-ը՝ համակարգի վրա ազդող արտաքին ուժերի համազորը: Այդ հավասարումից էլ հետևում է. եթե $F$$= 0$, որը նշանակում է՝ համակարգը փակ է, կամ նրա վրա արտաքին ազդեցությունները համակշռված են:

Δ \vec{p}

$= 0$, նշանակում է՝ համակարգի իմպուլսը չի փոխվել:

Ուշադրություն

Ուրեմն իրոք՝ փակ համակարգ կազմող մարմինների իմպուլսների գումարը պահպանվում է:

Մասնավորապես, $m1$ և $m2$ զանգվածներով մարմինների փակ համակարգի համար իմպուլսի պահպանման օրենքն ունի հետևյալ տեսքը.

m_{1} \vec{v_{1}} + m_{2} \vec{v_{2}} = m_{1} \vec{v_{1}^{՛}} + m_{2} \vec{v_{2}^{՛}}, որտեղ \vec{v_{1}} և \vec{v_{2}} մարմինների արագություններն են մինչև դրանց փոխազդեցությունը, իսկ \vec{v_{1}^{՛}} և \vec{v_{2}^{՛}} ՝ փոխազդեցությունից հետո

Շատ հաճախ մարմինների բախումները և պայթյունները (այդ թվում՝ կրակոցները) այնքան արագ են տեղի ունենում, որ գործնականորեն դրանց տևողությունը կարելի է համարել հավասար զրոյի: Բայց հավասարումից հետևում է, որ եթե $t = 0$,

ապա

Δ \vec{p}

$= 0$, այսինքն՝ իմպուլսը պահպանվում է: Ուրեմն, նշված դեպքերում կարելի է համարել, որ իմպուլսը պահպանվում է, նույնիսկ եթե համակարգը փակ չէ:

Ուշադրություն

Իմպուլսի պահպանման օրենքի փորձնական պացույցներից .

Ինչքան պակասում է առաջին գնդի իմպուլսը, նույնքան էլ աճում է վերջին գնդինը, փոխանցվելով մյուս գնդերով։ Գնդերի ընդհանուր (գումարային) իմպուլսը մնում է անփոփոխ, այսինքն` պահպանվում է։

Ռեակտիվ շարժում

Երկու մարմինների փոխազդեցության արդյունքի վերլուծությունը իմպուլսի պահպանման օրենքի տեսանկյունից ծնել է մի գաղափար, որի գործնական կիրառությունը հետագայում հսկայական դեր է խաղացել քաղաքակրթության զարգացման գործում: Բերենք մի օրինակ.

Լճափին կայանած նավակից զբոսաշրջիկը $m$ զանգվածով ուսապարկը հորիզոնական ուղղված $u$ արագությամբ նետում է դեպի ափը` նրան հաղորդելով $m$

\vec{u}

իմպուլս (տե՛ս նկար):

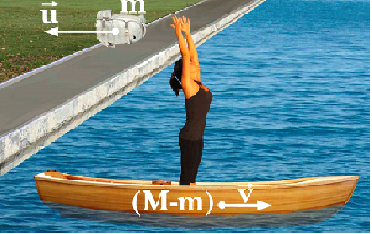
Նավակի, զբոսաշրջիկի և ուսապարկի ընդհանուր զանգվածը նշանակենք $M$-ով: Այդ մարմինները գործնականում կազմում են փակ համակարգ, որովհետև նրանց վրա արտաքին ազդեցությունները (Երկրի ձգողության և ջրի կողմից ազդող արքիմեդյան ուժերը) համակշռված են: Ուրեմն այդ համակարգի իմպուլսը պահպանվում է: Մինչ ուսապարկը նետելը այն եղել է զրո: Որպեսզի ուսապարկը նետելուց հետո էլ համակարգի իմպուլսը լինի զրո, համակարգի մնացած մասը (նավակը և զբոսաշրջիկը), որի զանգվածը դառնում է $M-m$, պետք է սկսի շարժվել այնպիսի

\vec{v}

արագությամբ, որ ուսապարկի և այդ մասի իմպուլսների գումարը լինի զրո.

m \vec{u} + (M - m) \vec{v} = 0, որտեղից \vec{v} = - \frac{m \vec{u}}{M - m}

Այս բանաձևում $«-»$ նշանը ցույց է տալիս, որ նավակը շարժվում է ուսապարկի շարժման հակառակ ուղղությամբ, իսկ նրա արագության մոդուլը որոշվում է $v = mu/(M-m)$ բանաձևով: Բանաձևից երևում է, որ համակարգի արագությունը կարելի է մեծացնել՝ մեծացնելով նետվող մարմնի զանգվածը և նետման արագությունը:

Ուշադրություն

Այսպիսով ստացվեց.

1. Երբ մարմնից նրա մի մասն անջատվում է որոշակի արագությամբ, մնացած մասը շարժվում է հակառակ ուղղությամբ:

2. Մեծացնելով անջատվող մասի զանգվածը և արագությունը, կարելի է մեծացնել մնացած մասի արագությունը:

Այս արդյունքը կարելի է օգտագործել շարժիչ ստեղծելու համար, ինչն այսօր հաջողությամբ իրականացվում է ամենատարբեր բնագավառներում՝ սկսած կենցաղից մինչև տիեզերագնացություն:

Պարզենք, թե վերը բերված օրինակում ո՞ր ուժն է շարժման մեջ դնում նավակը: Ուսապարկը նետելիս զբոսաշրջիկը նրա վրա ազդում է որոշակի ուժով: Նյուտոնի $III$ օրենքի համաձայն՝ ուսապարկը հակազդում է մոդուլով այդ ուժին հավասար և ուղղությամբ հակադիր ուժով: Հակազդեցության այդ ուժն էլ շարժման մեջ է դնում նավակը: Հակազդեցության ուժն անվանում են նաև ռեակցիայի ուժ, ուստի նավակի շարժումն անվանում են ռեակտիվ շարժում:

Ռեակտիվ շարժում են անվանում այն շարժումը, որի դեպքում մարմնից որոշակի արագությամբ նրա մի մասի անջատման հետևանքով մնացած մասը շարժվում է հակառակ ուղղությամբ:

Մարմնից անջատվող մասը կարող է լինել ինչպես պինդ մարմին, այնպես էլ հեղուկ կամ գազ: Հեղուկի արտանետման դեպքում առաջացող ռեակտիվ շարժումը կարելի է դիտել հետևյալ փորձով։ $45°$ անկյան տակ ծռված ծայրակալ ունեցող ռետինե փողրակին միացած ապակե ձագարի մեջ ջուր լցնենք (տե՛ս նկար)։ Հենց որ ջուրն սկսի դուրս թափվել ծայրակալից, փողրակը կսկսի շարժվել և կթեքվի ջրի հոսքին հակառակ ուղղությամբ։

Ուշադրություն

Ռեակտիվ շարժիչը մի սարք է, որից մեծ արագությամբ դուրս են նետվում վառելանյութի այրման ժամանակ առաջացած գազերը: Դրանք տեղակայվում են զանազան փոխադրամիջոցներում՝ հեծանիվ, ավտոմեքենա, գնացք, ինքնաթիռ, հրթիռ և այլն:

Սա ռեակտիվ շարժման գլխավոր առանձնահատկությունն է:

Թվարկված բոլոր փոխադրամիջոցներում քարշի ուժն առաջանում է առանց շրջապատի մարմինների հետ որևէ փոխազդեցության: Այն առաջանում է շնորհիվ համակարգի առանձին մասերի փոխազդեցության:

Ռեակտիվ շարժիչների շնորհիվ հրթիռը կարողանում է դուրս գալ տիեզերական տարածություն, որտեղ ռեակտիվ շարժիչներն առայսօր այլընտրանք չունեն:

Ռեակտիվ շարժումը բնության մեջ և տեխնիկայում.

Աղբյուրները

Ս. Վ. Գրոմով , Ն. Ա. Ռոդինա, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք ( I, II, III և V գլուխների հեղինակ Ա. Մամյան); Երևան, Անտարես -2014 թ.

2. Է. Ղազարյան, Ա. Կիրակոսյան, Գ. Մելիքյան, Ռ. Թոսունյան, Ս. Մաիլյան, Ֆիզիկա-8, հանրակրթական դպրոցի դասագիրք; Երևան, Էդիտ Պրինտ -2008 թ

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Մարմնի իմպուլս:Իմպուլսի պահպանման օրենքը: Ռեակտիվ շարժում

Տեսություն