Անկյան ռադիանային չափը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Անկյան ռադիանային չափը

Եռանկյունաչափության դասընթացից ծանոթ ենք անկյան աստիճանային չափին՝

1 °

մեծությամբ անկյունը փռված անկյան

\frac{1}{180}

մասն է:

Ծանոթանանք անկյունների չափման նոր միավորին՝ ռադիանին:

Ռադիանը կրճատ գրում են ռադ:

Դիտարկենք միավոր (կամ ցանկացած այլ շառավղով) շրջանագիծը:

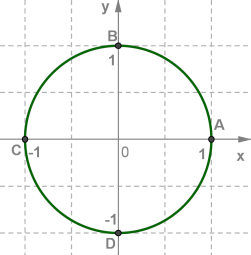
Ռադիանը անկյան չափման այն միավորն է, երբ

π ռադ = 180 °

Այս հավասարությունից ստանում ենք՝

1 ռադ = \frac{180 °}{π} \approx 57 °

Գիտենք, որ \(R\) շառավղով շրջանագծի երկարությունը հավասար է

l = 2 π \cdot R

Միավոր շրջանագծի երկարությունը կլինի՝

2 π \cdot 1 = 2 π

, համապատասխանում է \(360°\) կենտրանական անկյանը,

Կիսաշրջանագծի երկարությունը կլինի՝

\frac{1}{2} \cdot 2 π = π

, համապատասխանում է \(180°\) կենտրանական անկյանը,

Շրջանագծի քառորդի երկարությունը կլինի՝

\frac{1}{4} \cdot 2 π = \frac{π}{2}

, համապատասխանում է \(90°\) կենտրանական անկյանը:

Նկատենք, որ շրջանագծի, նրա կեսի և քառորդի երկարությունները համապատասխան կենտրոնական անկյունների վրա հենված աղեղների երկարություններն են:

Իսկ ո՞ր կենտրոնական անկյանն է համապատասխանում \(l\) երկարությամբ աղեղի երկարությունը: Նշանակենք այդ անկյունը

α

-ով և գտնենք այն:

\begin{array}{l} Քանի որ 360 ° \sim 2 π և α ° \sim 1, ապա \\ α ° = \frac{360 °}{2 π} = \frac{180 °}{π} \end{array}

Հիշենք, որ

1 ռադ = \frac{180 °}{π}

Հետևաբար,

α

-ն այն անկյունն է, որի ռադիանային չափը \(l\) ռադիան է:

Այսպիսով, մեկ ռադիան մեծությամբ անկյունն այն կենտրոնական անկյունն է, որի հենման աղեղի երկարությունը հավասար է շրջանագծի շառավղին:

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

2. Անկյան ռադիանային չափը