Տանգենսի ու կոտանգենսի արժեքները — դաս։ Հանրահաշիվ, 10-րդ դասարան.

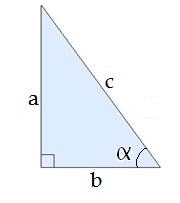
Ուղղանկյուն եռանկյան սուր անկյան տանգենսը և կոտանգենսը սահմանվում են հետևյալ կերպ՝

\begin{array}{l} tg α = \frac{դիմացի էջ}{կից էջ} tg α = \frac{a}{b} \\ ctg α = \frac{կից էջ}{դիմացի էջ} ctg α = \frac{b}{a} \end{array}

Տանգենսի արժեքը ստանալու համար պետք է միավոր շրջանագծին շոշափող տանել $(1;0)$ կետում: Տանգենսի արժեքները գտնվում են $Oy$ առանցքի վրա: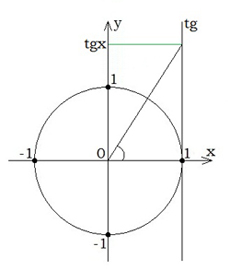
Կոտանգենսի արժեքը ստանալու համար պետք է միավոր շրջանագծին շոշափող տանել $(0;1)$ կետում: Կոտանգենսի արժեքները գտնվում են $Ox$ առանցքի վրա: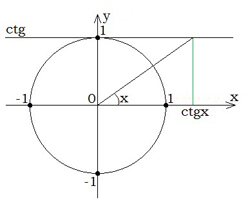

Տանգենսի և կոտանգենսի արժեքները հաշվում ենք արդեն ծանոթ բանաձևերի միջոցով՝

tg α = \frac{\sin α}{\cos α}

ctg α = \frac{\cos α}{\sin α}

Կարևոր է հիշել տանգենսի և կոտանգենսի հետևյալ արժեքները:

$tg 0° = 0$

$tg 90°$ գոյություն չունի

$tg 180° = 0$

$tg 270°$ գոյություն չունի

$tg 360° = 0$

$ctg 0°$ գոյություն չունի

$ctg 90° = 0$

$ctg 180°$ գոյություն չունի

$ctg 270° = 0$

$ctg 360°$ գոյություն չունի

Եռանկյունաչափական ֆունկցիաների հետևյալ արժեքները պետք է անգիր իմանալ:

Ցանկացած

α

անկյան համար տեղի ունեն հետևյալ բանաձևերը՝

tg (- α) = - tg α, ctg (- α) = - ctg α

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

3. Տանգենսի ու կոտանգենսի արժեքները