կետը կոչվում է \(y=f(x)\) ֆունկցիայի մաքսիմումի կետ, եթե գոյություն ունի կետը պարունակող այնպիսի միջակայք, որին պատկանող կամայական \(x\)-ի համար տեղի ունի անհավասարությունը:
Այդ դեպքում գրում են
Ֆունկցիայի արժեքը մաքսիմումի կետում կոչվում է ֆունկցիայի մաքսիմում և նշանակվում է
կետը կոչվում է \(y=f(x)\) ֆունկցիայի մինիմումի կետ, եթե գոյություն ունի կետը պարունակող այնպիսի միջակայք, որին պատկանող կամայական \(x\)-ի համար տեղի ունի անհավասարությունը:
Այդ դեպքում գրում են
Ֆունկցիայի արժեքը մինիմումի կետում կոչվում է ֆունկցիայի մինիմում և նշանակվում
Ֆունկցիայի մաքսիմումի և մինիմումի կետերը ունեն ընդհանուր անվանում՝ էքստրեմումի կետեր: Իսկ ֆունկցիայի մաքսիմումներն ու մինիմումները կոչվում են ֆունկցիայի էքստրեմումներ:
Դիտարկենք հետևյալ գրաֆիկը:
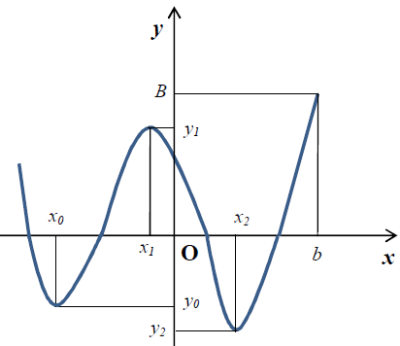
Այս ֆունկցիան ունի էքստրեմումի երեք կետ՝ -ն, -ը և -ը:
Ընդ որում, -ն և -ը մինիմումի կետեր են, իսկ -ը մաքսիմումի կետ է:
Ֆունկցիան իր փոքրագույն արժեքը՝ -ը ընդունում է -ը մինիմումի կետում:
Ֆունկցիայի մեծագույն արժեքը -ն է:
Սակայն ֆունկցիան իր մեծագույն արժեքը ընդունում է ոչ թե մաքսիմումի կետում, այլ ծայրակետում:
Հատվածում որոշված ֆունկցիան իր մեծագույն (փոքրագույն) արժեքը կարող է ընդունել մաքսիմումի (մինիմումի) կետում կամ հատվածի ծայրակետերում:
Աղբյուրները
Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:


