Թվային ֆունկցիայի գրաֆիկը — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Թվային ֆունկցիաներ ուսումնասիրելիս կարևոր է կարողանալ օգտվել նրա գրաֆիկից:

y = f (x), x \in X

ֆունկցիայի գրաֆիկ անվանում են կոորդինատային հարթության այն \((x; y)\) կետերի բազմությունը, որոնց համար

y = f (x)

Օրինակ

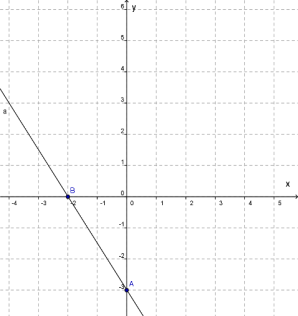
1. \(y=kx+b\) գծային ֆունկցիայի գրաֆիկն ուղիղ գիծ է:

Ներքևում ցուցադրված է

y = - 1,5 x - 3

ֆունկցիայի գրաֆիկը:

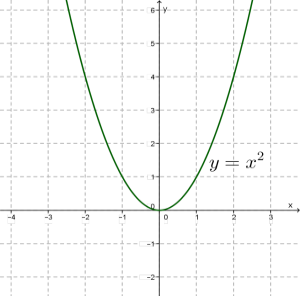
2. \(y=x²\) ֆունկցիայի գրաֆիկը կոչվում է պարաբոլ: Նրա տեսքը ցուցադրված է ներքևի նկարում:

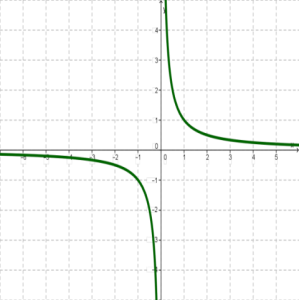
3. \(y=1/x\) ֆունկցիայի գրաֆիկը կոչվում է հիպերբոլ: Նրա տեսքը ցուցադրված է ներքևի նկարում:

y = \sqrt{x}

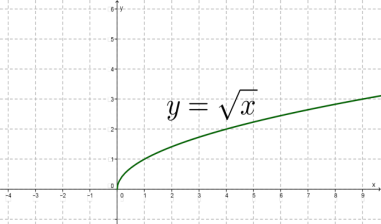
ֆունկցիայի գրաֆիկն ունի հետևյալ տեսքը:

5. Հիշենք նաև

y = |x|

ֆունկցիայի գրաֆիկը:

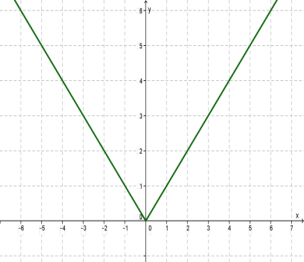
Հիշենք, որ ֆունկցիան ցանկացած արգումենտի համար պեքտ է ունենա միայն մեկ արժեք: Գրաֆիկի տերմիններով այս պահանջը նշանակում է, հետևյալը՝

Կոորդինատային հարթության վրա գտնվող կորը հանդիսանում է որևէ ֆունկցիայի գրաֆիկ այն և միայն այն դեպքում, եթե օրդինատների առանցքին զուգահեռ ցանկացած ուղիղ կամ կորը չի հատում կամ հատում է միայն մեկ կետում:

Օրինակ

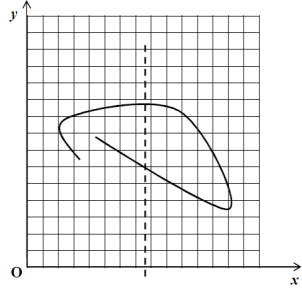
Ի տարբերություն վերևի կորերի, հետևյալ կորը որևէ ֆունկցիայի գրաֆիկ չէ (կետագծով նշված ուղիղը պատկերված կորը հատում է երկու կետերում):

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Թվային ֆունկցիայի գրաֆիկը

Տեսություն