1) \(y=f(x)\), ֆունկցիան անվանում են զույգ, եթե ցանկացած \(x\)-ի համար \(X\) բազմությունից կատարվում է հավասարությունը:
2) \(y=f(x)\), ֆունկցիան անվանում են կենտ, եթե ցանկացած \(x\)-ի համար \(X\) բազմությունից կատարվում է հավասարությունը:
2) \(y=f(x)\), ֆունկցիան անվանում են կենտ, եթե ցանկացած \(x\)-ի համար \(X\) բազմությունից կատարվում է հավասարությունը:
Ֆունկցիան կարող է լինել զույգ, կենտ, կարող է նաև լինել ո՛չ զույգ, ո՛չ էլ կենտ:
Այս հարցերի ուսումնասիրումը անվանում են ֆունկցիայի զույգության հետազոտում:
Եթե \(y=f(x)\) ֆունկցիան զույգ է կամ կենտ, ապա նրա \(D(f)\) որոշման տիրույթը համաչափ բազմություն է կոորդինատների սկզբնակետի նկատմամբ:
\(y=f(x)\) ֆունկցիայի զույգության հետազոտման ալգորիթմը
2. Կազմել \(f(-x)\) արտահայտությունը:
3. Համեմատել \(f(-x)\) և \(f(x)\) արտահայտությունները:
ա) Եթե ցանկացած արգումենտի համար, ապա ֆունկցիան զույգ է:
բ) Եթե ցանկացած , արգումենտի համար, ապա ֆունկցիան կենտ է:
գ) Եթե գոնե մեկ արգումենտի համար տեղի ունի կամ հավասարություններից մեկը, ապա \(y=f(x)\) ֆունկցիան ո՛չ զույգ է, ո՛չ էլ կենտ:
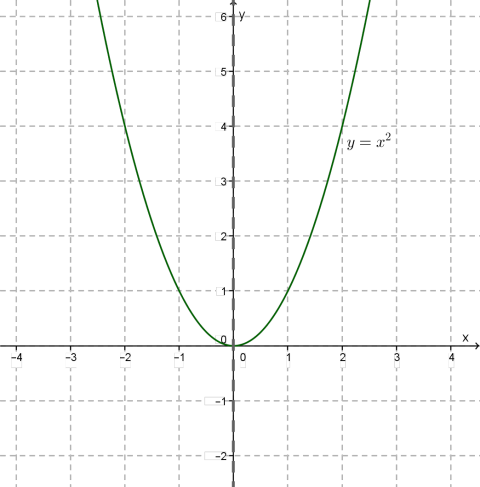
Եթե \(y=f(x)\) ֆունկցիայի գրաֆիկը համաչափ է օրդինատների առանցքի նկատմամբ, ապա ֆունկցիան զույգ է:
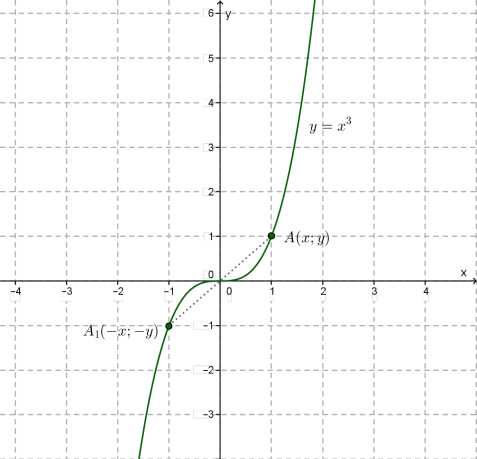
Եթե \(y=f(x)\) ֆունկցիայի գրաֆիկը համաչափ է կոորդինատների սկզբնակետի նկատմամբ, ապա ֆունկցիան կենտ է:
Սինուսը, տանգենսը, կոտանգենսը կենտ ֆունկցիաներ են, իսկ կոսինուսը զույգ ֆունկցիա է:
Աղբյուրները
Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:


