Միանդամ և դրա կատարյալ տեսքը

Թվերի փոփոխականների և դրանց աստիճանների արտադրյալը կոչվում է միանդամ:

Մեզ արդեն ծանոթ միանդամներ`


$x \cdot x = x^{2}$	$a \cdot a \cdot b = a^{2} b$	$3 x \cdot 5 x = (3 \cdot 5) \cdot (x \cdot x) = 15 x^{2}$

6 \cdot a \cdot y = 6 ay

0,25 x^{3}

abbc

8,43

16 c \cdot (- \frac{1}{2}) d

\frac{3}{8} x^{2} y

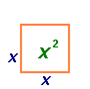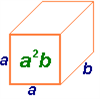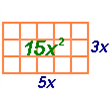արտահայտությունները ևս միանդամներ են:

Միանդամների գրառման ընթացքում թվերի և փոփոխականների միջև բազմապատկման նշան չի դրվում`

6 \cdot a \cdot y = 6 ay

Միանդամ են համարվում նաև հետևյալ արտահայտությունները.

- Մեկ փոփոխական, օրինակ՝ $x$-ը, քանի որ՝

x = 1 \cdot x

- Թիվ, օրինակ՝$3$ -ը, քանի որ՝

3 = 3 \cdot x^{0}

(թիվը ևս միանդամ է):

Որոշ միանդամներ կարելի է պարզեցնել: Օգտագործելով աստիճանների բազմապատկման հատկությունը` պարզեցնենք

6 x y^{2} \cdot (- 2) x^{3} y

արտահայտությունը:

a^{m} \cdot a^{n} = a^{m + n}

6 x y^{2} \cdot (- 2) x^{3} y

$=$

6 \cdot (- 2) x x^{3} y^{2} y = - 12 x^{4} y^{3}

(թվերը բազմապատկվում են, իսկ նույն տառերի ցուցիչները գումարվում են):

Միանդամի կատարյալ տեսք

Եթե միանդամում առաջինը գրված է թվային արտադրիչը, իսկ միևնույն փոփոխականների աստիճանների արտադրյալը գրված է մեկ աստիճանի տեսքով, ապա միանդամի այդպիսի տեսքը կոչվում է կատարյալ:

Միանդամը գրված է կատարյալ տեսքով, եթե՝

- միևնույն փոփոխականների արտադրյալը գրված է աստիճանի տեսքով,

- թվային արտադրիչը՝ միանդամի գործակիցը, միանդամում գրված է առաջին արտադրիչի տեղում:

10 \cdot \frac{1}{2} abbb

միանդամի կատարյալ տեսքը հետևյալն է՝

\frac{10 \cdot 1}{2} abbb = \frac{5 \cdot 2 \cdot 1}{2} a b^{3} = 5 a b^{3}

Կատարյալ տեսքով գրված միանդամի թվային արտադրիչը կոչվում է միանդամի գործակից:

Գործակիցները բազմապատկվում են իրար հետ, իսկ փոփոխականները՝ իրար հետ:

5 a b^{3}

միանդամի գործակիցը հավասար է $5$-ի, իսկ

- 12 x^{4} y^{3}

միանդամի գործակիցը հավասար է $-12$-ի:

$1$ և $-1$ գործակիցները սովորաբար չեն գրվում.

1 a^{2} y = a^{2} y

- 1 x^{3} = - x^{3}

Միանդամի աստիճան կոչվում է բոլոր փոփոխականների աստիճանների գումարը:

Միանդամի աստիճանը որոշելու համար պետք է գումարել բոլոր փոփոխականների (տառերի) աստիճանների ցուցիչները:

- 12 x^{4} y^{3}

արտահայտությունը հանդիսանում է յոթերորդ ($4 + 3 = 7$) աստիճանի միանդամ:

$6a$-ն առաջին աստիճանի միանդամ է ($a$ փոփոխականը առաջին աստիճանում է):
$7$-ը զրո աստիճանի միանդամ է:

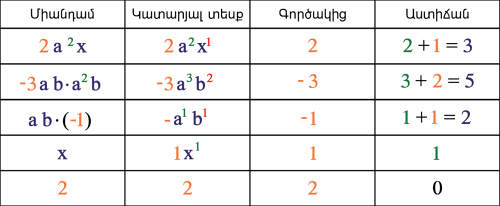
Նման միանդամներ

Ոչ զրոյական միանդամներն անվանում են նման, եթե կատարյալ տեսքի բերելուց հետո դրանք իրար հավասար են կամ տարբերվում են միայն իրենց գործակիցներով:

Նման են հետևյալ միանդամները՝

3 x^{2} y

- 4 x^{2} y

3 bab

2 a b^{2}

6 xy

xy

, $5$ և $-3$,

x

\frac{1}{3} x

Նման չեն հետևյալ միանդամները՝

y^{2} x

x^{2} y

Եթե նման միանդամներն ունեն հավասար գործակիցներ, ապա դրանք իրար հավասար են:

Դրանում կարելի է համոզվել միանդամները կատարյալ տեսքի բերելով:

Այս

8 x y^{3}, x y^{3}, 8 y^{3} x, 2 x \cdot 4 xyyy, 8 x^{3} y

միանդամներից իրար հավասար են՝

8 x y^{3}, 8 y^{3} x, 2 x \cdot 4 xyyy

միանդամները:

Դրանում կարելի է համոզվել, եթե բոլոր միանդամները գրենք կատարյալ տեսքով:

8 x y^{3}, x y^{3}, 8 y^{3} x, 2 x \cdot 4 xyyy, 8 x^{3} y

$=>$

8 x y^{3}, x y^{3}, 8 {x y}^{3}, 8 {x y}^{3}, 8 x^{3} y

Եթե նման միանդամների գործակիցները հակադիր թվեր են, ապա միանդամները կոչվում են հակադիր:

Այս

3 ac, - 9 ab, - 3 ac, abc, 9 ba

միանդամներից հակադիր են

3 ac և - 3 ac, 9 ba և - 9 ba

միանդամները:

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 7-րդ դասարան, Անտարես, 2011:

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

2. Միանդամ և դրա կատարյալ տեսքը

Տեսություն