Նման անդամների միացում

Գումարել և հանել կարելի է միայն նման միանդամները:

Ոչ զրոյական միանդամներն անվանում են նման, եթե կատարյալ տեսքի բերելուց հետո դրանք իրար հավասար են կամ տարբերվում են միայն իրենց գործակիցներով:

Նման միանդամները գումարելիս կամ հանելիս պետք է կատարել հետևյալ գործողությունները.

1. գումարել կամ հանել միանդամների գործակիցները,

2. տառերով արտադրիչները չփոփոխել:

$2 x^{3} + 3 x^{3} = 5 x^{3}$
$4 a b^{2} - a b^{2} = 3 a b^{2}$

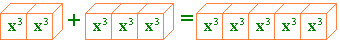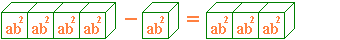Նման միանդամների գումարը հավասար է մի միանդամի, որը նման է դրանցից յուրաքանչյուրին և գործակիցը հավասար է այդ միանդամների գործակիցների գումարին:

Օրինակներ՝

3 a^{2} b + 2 a^{2} b = (3 + 2) a^{2} b = 5 a^{2} b

5 x^{3} y^{2} + (- 2) x^{3} y^{2} = (5 - 2) x^{3} y^{2} = 3 x^{3} y^{2}

Նման միանդամների տարբերությունը հավասար է մի միանդամի, որը նման է դրանցից յուրաքանչյուրին և գործակիցը հավասար է այդ միանդամների գործակիցների տարբերությանը:

Օրինակ՝

2 x^{4} y - 7 x^{4} y = (2 - 7) x^{4} y = - 5 x^{4} y

Նման միանդամների գումարի փոխարինումը նրանց գումար հանդիսացող միանդամով անվանում են նման անդամների միացում:

Ուշադրություն

Հաճախ նման անդամների միացում կատարելիս պետք է լինում փակագծերը բացել:

Եթե փակագծից առաջ կանգնած է մինուս նշանը, ապա փակագծերը բացելիս միանդամի գործակցի նշանը փոխվում է:

Օրինակ՝

- (- 0,6 p^{3} k) = 0,6 p^{3} k

Ուշադրություն

Միանդամների գումարման կամ հանման ժամանակ պետք է հիշել, որ՝

- չի կարելի գումարել կամ հանել այնպիսի միանդամներ, որոնց փոփոխականների արտադրյալները տարբերվում են,

- հակադիր միանդամների գումարը հավասար է $0$-ի:

Օրինակ՝ միանդամների այս

3 uv - 2 u v^{2}

հանումը չի կարելի կատարել, քանի որ փոփոխականների արտադրյալները տարբերվում են իրարից (միանդամները նման չեն):

\frac{1}{2} b^{3} c - \frac{1}{2} b^{3} c = 0

, քանի որ հակադիր միանդամների գումարը միշտ հավասար է $0$-ի:

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 7-րդ դասարան, Անտարես, 2011:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Նման անդամների միացում

Տեսություն