Հանրահաշվական կոտորակների հիմնական հատկությունը

Թվային կոտորակների հիմնական հատկությունը

Թվային կոտորակի արժեքը չի փոխվի, եթե նրա համարիչը և հայտարարը բազմապատկենք զրոյից տարբեր ցանկացած թվով:

Կոտորակի համարիչի և հայտարարի նույն թվի վրա բաժանելը կոչվում է կոտորակի կրճատում:

1.		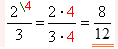Համարիչը և հայտարարը բազմապատկեցինք $4$-ով:
2.		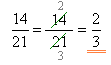Համարիչը և հայտարարը բաժանեցինք $7$-ի, այսինքն՝ $\frac{14}{21}$ կոտորակը կրճատեցինք $7$-ով:

Հանրահաշվական կոտորակների դեպքում ևս այս հատկությունը մնում է ուժի մեջ:

Հանրահաշվական կոտորակների հիմնական հատկությունը

Հանրահաշվական կոտորակի արժեքը չի փոխվի, եթե նրա համարիչը և հայտարարը բազմապատկենք միևնույն արտահայտությամբ, որի արժեքը զրոյից տարբեր է:

1.		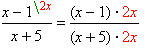Համարիչը և հայտարարը բազմապատկեցինք $2x$ միանդամով:
2.		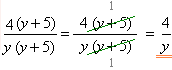Համարիչը և հայտարարը բաժանեցինք $y + 5$ երկանդամի վրա, այսինքն՝ $\frac{4 (y + 5)}{y (y + 5)}$ կոտորակը կրճատեցինք $y + 5$-ով:

Ուշադրություն

Հանրահաշվական կոտորակների հետ գործողություններ կատարելիս միշտ ենթադրվում է, որ գործողությունները կատարվում են որոշման տիրույթում (թույլատրելի արժեքների հետ):

Օրինակ

Կրճատիր

\frac{26 abc}{169 ac}

կոտորակը:

1. $26$ և $169$ կոտորակներն ունեն $13$ ընդհանուր բազմապատիկը: Այդ պատճառով կոտորակը կարելի է կրճատել՝

\frac{26 a^{3} b c^{2}}{169 a^{3} c} = \frac{2 \cdot 13 a^{3} bc}{13 \cdot 13 a^{2} c} = \frac{2 a^{3} bc}{13 a^{2} c}

2. Կրճատվում են նույն հիմքով աստիճանները՝

\frac{a^{3}}{a^{2}} = \frac{a^{2 + 1}}{a^{2}} = \frac{a^{2} \cdot a^{1}}{a^{2}} = \frac{a^{1}}{1} = a^{1}

2.1

a^{3}

a^{2}

աստիճանները կրճատվում են փոքր աստիճանի՝

a^{2}

-ով՝

\frac{2 a^{3} bc}{13 a^{2} c} = \frac{2 a^{3} bc}{13 a^{2} c} = \frac{2 abc}{13 c}

2.2 Կրճատվում են $c$ հավասար արտադրիչները: $b$ փոփոխականը չի կարելի կրճատել, քանի որ հայտարարում այն չկա:

\frac{2 abc}{13 c} = \frac{2 ab c}{13 c} = \frac{2 ab}{13}

Պատասխան՝ կրճատելով

\frac{26 abc}{169 ac}

կոտորակը, ստանում ենք՝

\frac{2 ab}{13} կամ \frac{2}{13} ab

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:

Վերադառնալ թեմային

Հաջորդ տեսությունը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Հանրահաշվական կոտորակների հիմնական հատկությունը

Տեսություն