ֆունկցիայի հատկությունները \(k > 0\) դեպքում
Այս ֆունկցիայի հատկությունները նկարագրելիս, կհիմնվենք նրա գրաֆիկի՝ հիպերբոլի վրա:
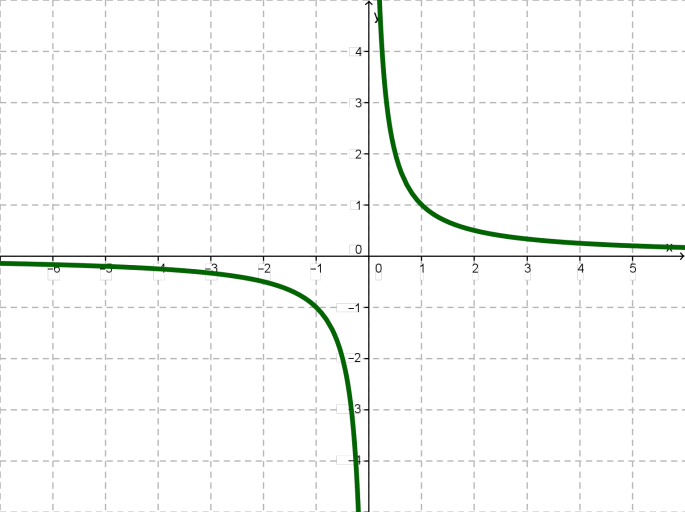
1. Ֆունկցիան որոշված է ցանկացած կետում, բացի \(x = 0\) կետից՝
2. Եթե \(x > 0\), ապա \(y > 0\): Եթե \(x < 0\), ապա \(y < 0\)
3. Ֆունկցիան նվազում է միջակայքերի վրա:
4. Ֆունկցիան ոչ վերևից, ոչ էլ ներքևից սահմանափակ չէ:
5. Ֆունկցիան չունի ոչ մեծագույն, ոչ էլ փոքրագույն արժեքներ:
6. Ֆունկցիան անընդհատ է միջակայքերում, իսկ \(x = 0\) կետում խզվում է:
Ուշադրություն
Հիպերբոլի առանձին ճյուղերը հնարավոր է նկարել մատիտի անընդհատ շարժումով: Սակայն ամբողջ հիպերբոլը (երկու ճյուղերը միասին) հնարավոր չէ նկարել առանց մատիտը թղթից պոկելու:
7. Ֆունկցիայի արժեքների բազմությունը օրդինատների ամբողջ առանցքն է, առանց \(y = 0\)
կետի՝
ֆունկցիայի հատկությունները \(k < 0\) դեպքում
Այս ֆունկցիայի հատկությունները նկարագրելիս, կհիմնվենք նրա գրաֆիկի՝ հիպերբոլի վրա:
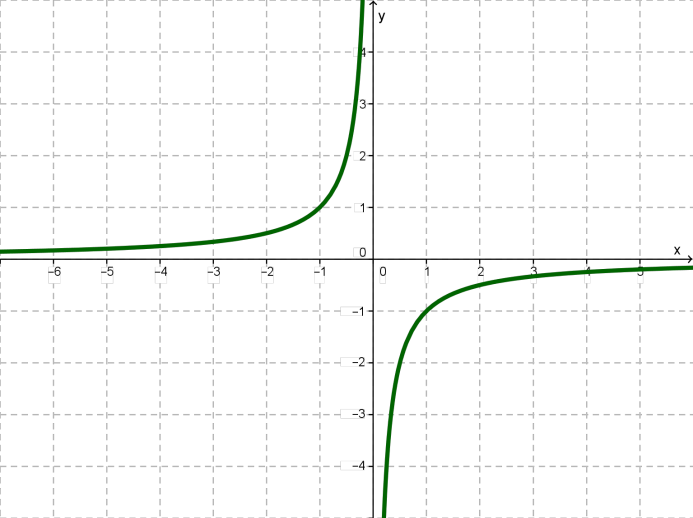
1. Ֆունկցիան որոշված է ցանկացած կետում, բացի \(x = 0\) կետից՝ :
2. Եթե \(x < 0\), ապա \(y > 0\): Եթե \(x > 0\), ապա \(y < 0\):
3. Ֆունկցիան աճում է միջակայքերի վրա:
4. Ֆունկցիան ոչ վերևից, ոչ էլ ներքևից սահմանափակ չէ:
5. Ֆունկցիան չունի ոչ մեծագույն, ոչ էլ փոքրագույն արժեքներ:
6. Ֆունկցիան անընդհատ է միջակայքերում, իսկ \(x = 0\) կետում խզվում է:
7. Ֆունկցիայի արժեքների բազմությունը օրդինատների ամբողջ առանցքն է, անանց \(y = 0\) կետի՝ :
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:


