Նշանի փոփոխման հատկությունը — դաս։ Հանրահաշիվ, 9-րդ դասարան.

Եթե ֆունկցիան տրվում է

f (x) = (x - x_{1}) (x - x_{2}) ... (x - x_{n})

բանաձևով, որտեղ

x

-ը փոփոխականն է, իսկ

x_{1}, x_{2}, ..., x_{n}

իրարից տարբեր թվեր են (ֆունկցիայի զրոներն են), ապա միջակայքերից յուրաքանչյուրում, որոնք առաջանում են այդ թվերով, ֆունկցիայի նշանը պահպանվում է, ընդ որում հարևան միջակայքերում ֆունկցիայի նշանները իրարից տարբեր են:

Այս հատկությունը օգտագործվում է անհավասարումների լուծման ժամանակ:

Օրինակ

Լուծենք

(x - 7) (x + 4) < 0

անհավասարումը:

Գտնենք ֆունկցիայի զրոները:

Ձախ մասը հավասարեցնենք զրոյի և հիշենք, որ արտադրյալը հավասար է զրոյի եթե զրոյի է հավասար արտադրիչներից գոնե մեկը:

\begin{array}{l} (x - 7) (x + 4) = 0 \\ x - 7 = 0 x + 4 = 0 \\ x_{1} = 7 x_{2} = - 4 \end{array}

Կոորդինատային ուղղի վրա նշենք գտած թվերը և պարզենք ֆունկցիայի նշանները առաջացած միջակայքերից յուրաքանչյուրում:

Բավական է պարզել ֆունկցիայի նշանը միջակայքերից որևէ մեկում՝ նշանները մյուսներում, ըստ բերված հատկության, կարելի է պարզել՝ հերթով փոխելով նշանները:

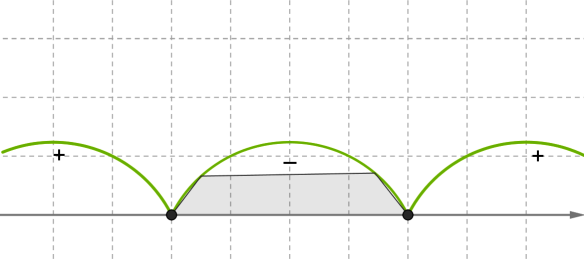
\(-\)4 7 \(x\)

(- 4; 7)

միջակայքից ընտրենք \(x=0\) կետը, ապա

(0 - 7) \cdot (0 + 4) = -28

\(<0\)

Մյուս երկու միջակայքերում ֆունկցիան կլինի դրական:

Մեզ պետք են

x

-ի այն արժեքները, որոնցում ֆունկցիան բացասական է: Հետևաբար, անհավասարման լուծումների բազմությունը

(- 4; 7)

միջակայքն է:

Պատասխան՝

x \in (- 4; 7)

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013:

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ