Ենթադրենք, թե դու պատրաստվում ես ելույթի «Եղանակը հունիսին» թեմայով:
Ամբողջ ամսվա ընթացքում դու հավաքել ես տվյալներ եղանակի, խոնավության և ճնշման վերաբերյալ: Ստացված տվյալները ներկայացրու հետևյալ աղյուսակի տեսքով (բերված է աղյուսակի մի մասը, հունիս ամսվա առաջին շաբաթվա վերաբերյալ):
Եղանակը \(2014\) թ. հունիսին
Ամսաթիվ | Ջերմաստիճան \((\)\()\) | Խոնավություն (%) | Ճնշում (մմ) |
\(1\) | \(+16\) | \(25\) | \(759\) |
\(2\) | \(+17\) | \(30\) | \(759\) |
\(3\) | \(+15\) | \(30\) | \(759\) |
\(4\) | \(+14\) | \(30\) | \(759\) |
\(5\) | \(+17\) | \(26\) | \(759\) |
\(6\) | \(+18\) | \(35\) | \(760\) |
\(7\) | \(+16\) | \(32\) | \(760\) |
Իհարկե, դու կարող ես աղյուսակը ներկայացնել ամբողջ ամսվա համար, գծել այն մեծ պաստառի վրա և ներկայացնել աշխարհագրության դասին: Բայց արդյո՞ք քո համադասարանցիները և ուսուցիչը կկարողանան ընկալել քո ներկայացրած տվյալները և պատկերացում կազմել հունիս ամսվա եղանակի մասին: Հավանաբար, ոչ:
Բանն այն է, որ քո ներկայացրած տվյալները, լինելով ամբողջական, հավաստի և լիարժեք, այնուամենայնիվ ակնառու չեն և, ըստ էության, հետաքրքիր չեն լինի քո ելույթը լսողների համար:
Ելույթն ավելի ակնառու և հեշտ ընկալելի կարելի է դարձնել, եթե օգտագործես գրաֆիկներ և դիագրամներ:
Շրջանաձև դիագրամներ
Դիագրամները ապահովում են ակնառու պատկերացում մեծությունների կախվածությունների վերաբերյալ:
Մեծությունների հարաբերության ներկայացումը շրջանի մասերի միջոցով կոչվում է շրջանաձև դիագրամ:
Ուշադրություն
Շրջանաձև դիագրամները օգտագործում են այն դեպքերում, երբ համեմատվող մեծությունների գումարը տալիս է \(100\) %:
Ներքևի դիագրամը ցույց չի տալիս որոշակի ամպամածությամբ օրերի քանակը:
Սակայն, այն ցույց է տալիս, թե այս կամ այն ամպամածությամբ օրերը ամբողջի քանի տոկոսն են կազմում:
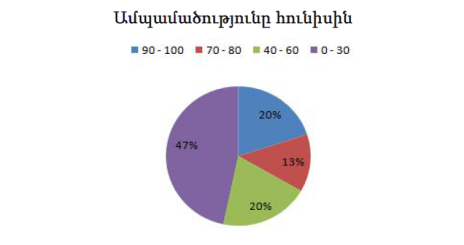
Որոշակի ամպամածությամբ օրերն ունեն իրենց գույնը և նույնիսկ առանց թվային արժեքների. կարելի է որոշակի պատկերացում կազմել ամսվա ընթացքում ամպամածության վերաբերյալ:
Շրջանաձև դիագրամների հիմնական առավելությունը ակնառու լինելն է:
Տվյալների ճշգրտությունն ապահովելու համար հաճախ օգտագործում են սյունակաձև դիագրամները:
Սյունակաձև դիագրամներ.
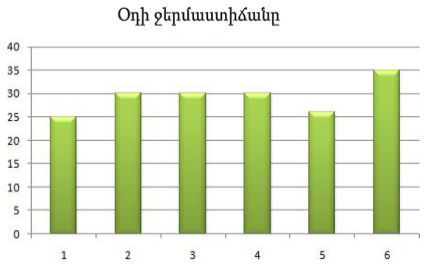
Սյունակաձև դիագրամները (սյունապատկերները) կազմված են նույն լայնությամբ զուգահեռ ուղղանկյուններից (սյունակներից): Յուրաքանչյուր սյունակ ցույց է տալիս տվյալների որոշակի տեսակ (օրինակ՝ ամպամածության տեսակը): Տվյալների տեսակները դասակարգված են հորիզոնական առանցքի վրա:
Սյունակի բարձրությունը ցույց է տալիս տվյալների որոշակի տեսակի արժեքը (օրինակ՝ որոշակի ամպամածությամբ օրերի քանակը):
Արժեքները տեղադրվում են ուղղահայաց առանցքի վրա:
Աղբյուրները
Բ. Նահապետյան, Ա. Աբրահամյան, Մաթեմատիկա 6-րդ դասարան, ՄԱՆՄԱՐ, 2012:


