Համեմատական հատվածներ — դաս։ Երկրաչափություն, 8-րդ դասարան.

Համեմատական հատվածներ

Հատվածների հարաբերություն կոչվում է նրանց երկարությունների հարաբերությունը:

Դիտարկենք \(AB\) և \(VN\) հատվածները, որտեղ \(АВ\) -ն \(2\) անգամ մեծ է երկրորդ հատվածից:

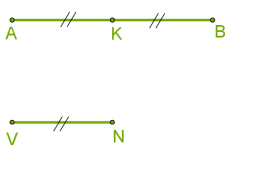
\(AB\) և \(VN\) հատվածների հարաբերությունը հավասար է \(2 : 1\)

\frac{AB}{VN} = \frac{2}{1}

Կարելի է նաև ասել, որ \(VN\) և \(AB\) հատվածների հարաբերությունը \(1 : 2\) է:

\frac{VN}{AB} = \frac{1}{2}

Հաջորդ օրինակում \(AR\) հատվածը հավասար է երեք միավորի, իսկ \(VZ\) հատվածը՝ երկու միավորի:

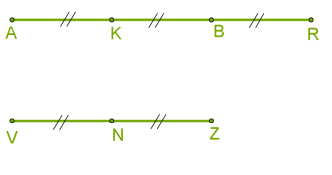
\(AR\) և \(VZ\) հատվածների հարաբերությունը \(3 : 2\) է:

\frac{AR}{VZ} = \frac{3}{2}

կամ՝

\frac{VZ}{AR} = \frac{2}{3}

Եթե \(a\) և \(b\) հատվածների երկարությունների հարաբերությունը հավասար է \(c\) և \(d\) հատվածների երկարությունների հարաբերությանը, այսինքն՝

\frac{a}{b} = \frac{c}{d}

, ապա այդ հատվածները կոչվում են համեմատական:

Համեմատենք վերևի հատվածների երկարությունները՝

\frac{AB}{VN} \neq \frac{AR}{VZ}

: Ստացանք, որ հատվածները համեմատական չեն:

Դիտարկենք հաջորդ նկարը:

Համեմատենք հատվածների երկարությունները՝

\frac{AB}{VN} և \frac{AH}{VT}

\frac{AB}{VN} = \frac{2}{1} և \frac{AH}{VT} = \frac{4^{2}}{2_{1}} = \frac{2}{1}

Ուրեմն,

\frac{AB}{VN} = \frac{AH}{VT}

: Այս հատվածների զույգերը համեմատական են:

Հատվածների հարաբերությունը գրելու համար պետք է երկու հատված: Համեմատական հատվածները գտնելու համար պետք է չորս հատված (հատվածների երկու զույգ):

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:

Սխա՞լ ես գտել

2. Համեմատական հատվածներ