Քառանկյան արտագծյալ շրջանագիծ
Եթե քառանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:
Այս հարցը պարզվում է հետևյալ պնդման միջոցով:
Եթե քառանկյանը արտագծվել է շրջանագիծ, ապա քառանկյան հանդիպակաց անկյունների գումարը \(180\) աստիճան է:
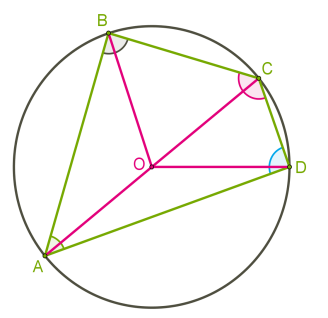
Քառանկյան բոլոր անկյունները շրջանագծի համար ներգծյալ անկյուններ են: Ուրեմն, դրանք հավասար են այն աղեղների կեսերին, որոնց վրա հենվում են: Հանդիպակաց անկյունները հենվում են երկու աղեղների վրա, որոնց միավորումը տալիս է ամբողջ շրջանագիծը՝ : Կեսը կլինի :
Այս հատկությունը կարելի է օգտագործել, որպես հայտանիշ, որի միջոցով կարելի է պարզել, թե ո՞ր քառանկյուններն ունեն արտագծյալ շրջանագիծ:
Եթե քառանկյան հանդիպակաց անկյունների գումարը \(180\) է, ապա նրան կարելի է արտագծել շրջանագիծ:
Ինքնուրույն պարզիր, թե ո՞ր քառանկյուններին (զուգահեռագիծ, այդ թվում նաև՝ քառակուսի, ուղղանկյուն, շեղանկյուն, սեղան, հավասարասրուն սեղան և ուղղանկյուն սեղան) կարելի է արտագծել շրջանագիծ:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:


