Գլանի ծավալը
Հիշենք, որ պրիզմայի ծավալը հավասար է հիմքի մակերեսի և բարձրության արտադրյալին՝
Հիմնավորենք, որ նույն կանոնը գործում է նաև գլանի դեպքում:
Դիցուք՝ \(r\) շառավղով և \(h\) բարձրությամբ գլանին ներգծված է կանոնավոր \(n\)-անկյուն պրիզմա:
Յուրաքանչյուր այդպիսի պրիզմայի ծավալը դիտարկվող գլանի ծավալի մոտավոր արժեքն է:
Որքան մեծ է \(n\)-ը, այնքան ճշգրիտ է մոտավոր արժեքը:
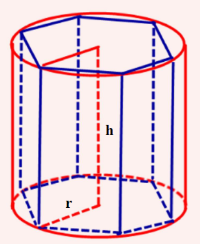
Պատկերացնենք, թե
\(n\)-ը անվերջ մեծացնելիս, պրիզմայի ծավալը «ձգտում է» գլանի ծավալին:
Քանի որ պրիզմայի ծավալը հավասար է հիմքի մակերեսի և բարձրության արտադրյալին, ապա նույնը տեղի է ունենում գլանի ծավալի դեպքում:
Այսպիսով, գլանի ծավալը հավասար է հիմքի մակերեսի և բարձրության արտադրյալին՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ», 2013


