1. Վեկտորների հանումը

Վեկտորների հանումը
Վեկտորների հանումը լավ հասկանալու համար հիշենք գումարման և հանման գործողությունների հատկությունները:
 
Եթե x+y=z, ապա x=z−y
 
Այս հատկությունը տեղի ունի նաև վեկտորների դեպքում:
a→ վեկտորից  b→ վեկտորը հանելու համար պետք է գտնել այնպիսի c→ վեկտոր, որի գումարը b→-ի հետ հավասար է  a→ վեկտորին:
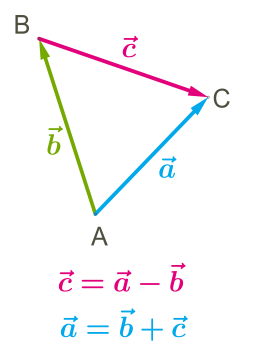
Atnemsana1.png
a→ վեկտորից b→ վեկտորները հանելու համար պետք է՝
 
1) վեկտորները տեղադրել նույն \(A\) սկզբնակետից,
2) միացնել դրանց \(B\) և \(C\) վերջնակետերը,
3) տարբերության վեկտորի ուղղությունն ընտրում ենք հանելիի վերջնակետից դեպի նվազելիի վերջնակետը: 
Հիշենք վեկտորների գումարման զուգահեռագծի կանոնը: Ըստ այդ կանոնի, զուգահեռագծի նույն գագաթից երկու կողմերի վրա դուրս եկող վեկտորների գումարը ընկած է զուգահեռագծի այդ գագաթից դուրս եկող անկյունագծի վրա:
 
Տարբերության վեկտորը այս դեպքում ընկած է մյուս անկյունագծի վրա:
 
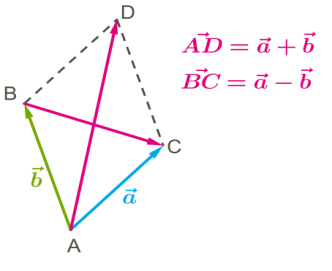
Atnemsana2.png
 
Նկատենք, որ b→ վեկտորից a→ վեկտորը հանելիս, տարբերության d→ վեկտորը հակադիր է c→ վեկտորին, այսինքն՝ d→=−c→
 
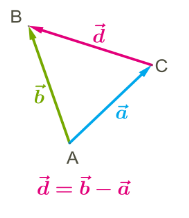
Atnemsana0.png
 
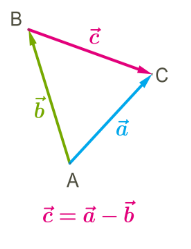
Atnemsana.png
 
Վեկտորների հանման գործողությունը կարելի է բերել արդեն դիտարկված գումարման գործողությանը:
a→ և b→ վեկտորի տարբերությունը հավասար է a→ վեկտորի և b→ վեկտորի −b→ հակադիր վեկտորի գումարին՝  a→−b→=a→+−b→
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի.Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, "Զանգակ", 2013:
Վերադառնալ թեմային
Հաջորդ առաջադրանքը
Copyright © 2026 ԻմԴպրոց ՍՊԸ