Թվային ֆունկցիա, տրման եղանակները
Դիցուք \(X\)-ը որևէ թվային բազմություն է: Եթե այդ բազմության յուրաքանչյուր \(x\) թվի որոշակի \(f\) օրենքով համապատասխանության մեջ է դրվում ճիշտ մեկ \(y\) թիվ, ապա ասում են, որ \(X\) բազմության վրա տրված է \(y = f(x)\) ֆունկցիան:
\(x\)-ը անվանում են անկախ փոփոխական կամ արգումենտ, իսկ \(y\)-ը՝ կախյալ փոփոխական կամ ֆունկցիայի արժեք: \(X\) բազմությունը անվանում են ֆունկցիայի որոշման տիրույթ:
\(x\)-ը անկախ փոփոխականն է, կամ արգումենտը,
\( \)
\(y\)-ը կախյալ փոփոխականն է, կամ ֆունկցիայի արժեքը \(x\) կետում,
\(f\)-ը կանոնն է, որով ամեն \(x\) արգումենտի համար գտնվում է ֆունկցիայի \(y\) արժեքը:
Ուշադրություն
Ֆունկցիան տալու համար պետք է նկարագրել \(f\) օրենքը (կանոնը, եղանակը), որի օգնությամբ \(X\) բազմության ցանկացած \(x\)-ի համար կարելի է գտնել ֆունկցիայի \(y\) արժեքը:
Օրինակ
Ֆունկցիայի օրինակ է \(x\) և \(y\) փոփոխականների միջև \(y = 2x\) առնչությունը:
Այս դեպքում կանոնը հետևյալն է՝ ցանկացած \(x\) թիվ պետք է կրկնապատկել, ստացված կրկնապատիկ թիվը՝ \(y=2x\)-ը կլինի ֆունկցիայի արժեքը \(x\) կետում:
Քանի որ ցանկացած թիվ կարելի է կրկնապատկել, ապա այս ֆունկցիան իմաստ ունի ցանկացած \(x\)-ի համար: Սա նշանակում է, որ ֆունկցիայի որոշման տիրույթը՝ \(X\) բազմությունը, ամբողջ թվային առանցքն է:
Այս օրինակում ֆունկցիան տրվում է բանաձևի \((y=2x)\) միջոցով: Գոյություն ունեն \(f \) օրենքը նկարագրելու (ֆունկցիայի տրման) այլ եղանակներ:
Ֆունկցիայի տրման եղանակները
1. Գրաֆիկական եղանակ: Ֆունկցիան տրվում է գրաֆիկի (դիագրամի, սյունապատկերի) միջոցով:
Եթե ունենք ֆունկցիան, և \(xOy\) հարթության վրա նշված են \((x; y)\) տեսքի բոլոր կետերը, որտեղ , և , ապա այդ կետերի բազմությունը կոչվում է ֆունկցիայի գրաֆիկ:
Օրինակ
\(y = kx՝ \)ուղիղ գիծ:
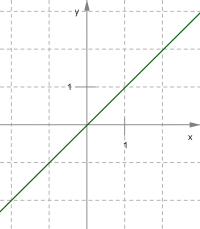
2. Անալիտիկ եղանակ: Ֆունկցիան տրվում է բանաձևի միջոցով:
3. Աղյուսակային եղանակ: Ֆունկցիան տրվում է աղյուսակի միջոցով:
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(y\) | \(1\) | \(4\) | \(9\) | \(16\) |
4. Թվազույգերի եղանակ: Ֆունկցիան տրվում է թվազույգերով՝
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 7-րդ դասարան, Անտարես, 2011:


