Հանրահաշվական կոտորակների կրճատումը
Հանրահաշվական կոտորակը կրճատելու համար պետք է կոտորակի համարիչը և հայտարարը վերլուծել արտադրիչների: Եթե պարզվի, որ համարիչն ու հայտարարն ունեն ընդհանուր արտադրիչներ, ապա դրանք կարելի է կրճատել:
Արտադրիչների վերլուծման օրինակներ՝
- ընդհանուր արտադրիչի դուրս բերումը փակագծերից,
- կրճատ բազմապատկման բանաձևերի օգտագործումը,
- խմբավորման եղանակ:
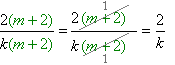 | - կոտորակը կրճատված է \((m + 2)\) երկանդամով |
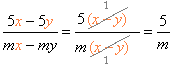 | - համարիչն ու հայտարարը վերլուծված են արտադրիչների, և կոտորակը կրճատված է \((x - y)\) ընդհանուր արտադրիչով |
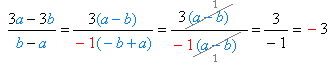 | - համարիչն ու հայտարարը վերլուծված են
արտադրիչների, և կոտորակը կրճատված է \((a - b)\) ընդհանուր արտադրիչով |
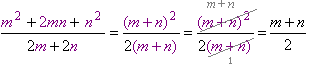 | - համարիչը վերլուծված է արտադրիչների գումարի քառակուսու բանաձևի միջոցով, հայտարարում փակագծերից դուրս է բերված ընդհանուր արտադրիչը, ապա կոտորակը կրճատված է \((m + n)\) երկանդամի վրա |
Կրճատ բազմապատկման բանաձևերը, որոնք օգտագործվում են կոտորակները կրճատելիս
Գումարի քառակուսի՝
Տարբերության քառակուսի՝
Խորանարդների գումար՝
Խորանարդների տարբերություն՝
Օրինակ
Կրճատենք հանրահաշվական կոտորակը:
Լուծում:
1. Կոտորակի համարիչն ու հայտարարը վերլուծում ենք արտադրիչների՝ օգտագործելով քառակուսիների տարբերության և տարբերության քառակուսու բանաձևերը:
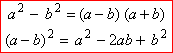 |
2. Կոտորակը կրճատում ենք \((x-2)\) ընդհանուր արտադրիչով:
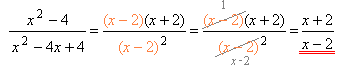
կոտորակը ձևափոխիր այնպես, որ հայտարարում առաջանա արտահայտությունը:
Լուծում:
1. կոտորակը ձևափոխելու համար վերլուծենք արտահայտությունը արտադրիչների՝
2. Համեմատում ենք ստացված արտադրյալը կոտորակի հայտարարի՝ \(x+2\) երկանդամի հետ և եզրակացնում ենք, որ պետք է համարիչը և հայտարարը բազմապատկել \(3(x-2)\) -ով:
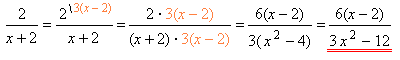
Պարզեցրու հանրահաշվական կոտորակը:
Լուծում:
1. Համարիչում փակագծերից դուրս բերենք \(2\)-ը, իսկ հայտարարում՝ \(6\)-ը:
2. արտահայտությունը վերլուծենք արտադրիչների խորանարդների գումարի բանաձևի օգնությամբ և կրճատենք կոտորակը:
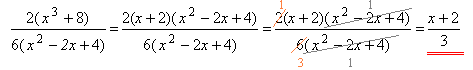
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:


