2. y=x² ֆունկցիայիi հատկությունները

 

 

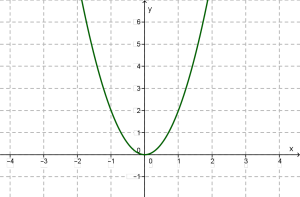
1. $y=x^2$ ֆունկցիան որոշված է բոլոր իրական թվերի համար՝ ֆունկցիայի որոշման տիրույթը ամբողջ թվային առանցքն է՝ $D=\left(-\mathrm{\infty };+\mathrm{\infty }\right)$

 

2. \(y = 0\) եթե \(x = 0\), \(у > 0\) եթե $x\ne 0$: Ֆունկցիան ընդունում է միայն դրական արժեքներ և միայն զրո կետում նրա արժեքը հավասար է զրոյի: Սա երևում է պարաբոլի տեսքից (ամբողջ գրաֆիկը գտնվում է \(x\))-երի առանցքից վեր):

Այս հատկությունը ակնհայտ է նաև առանց գրաֆիկի օգնության: Իրոք, եթե $x\ne 0$, ապա $x^2>0$

 

3. $y=x^2$ ֆունկցիան անընդհատ է ամբողջ թվային առանցքի վրա: 

 

4. Ֆունկցիայի փոքրագույն արժեքը \(0\) -ն է՝  $y_{\mathit{min}}=0$ (հասնում է \(х = 0\) կետում) և չունի մեծագույն արժեք՝  $y_{\mathit{max}}$  գոյություն չունի: 

 

5. $y=x^2$ ֆունկցիան սահմանափակ է ներքևից և սահմանափակ չէ վերևից:

 

6. $y=x^2$ ֆունկցիան նվազում է $\left(-\mathrm{\infty };\left.0\right]\right.$ ճառագայթի վրա և աճում է $\left[0;\left.+\mathrm{\infty }\right)\right.$ ճառագայթի վրա:

 

7. $y=x^2$ ֆունկցիայի արժեքների բազմությունը օրդինատների առանցքի դրական ճառագայթն է՝ $\left[0;\left.+\mathrm{\infty }\right)\right.$

 

Հինգերորդ հատկության մեջ խոսվում է ֆունկցիայի սահմանափակության մասին: Սահմանենք այդ գաղափարը:

Նայելով $y=x^2$ ֆունկցիայի գրաֆիկին, տեսնում ենք, որ այն ընկած է, օրինակ՝ \(у = -1\) ուղղից վեր:

 

 

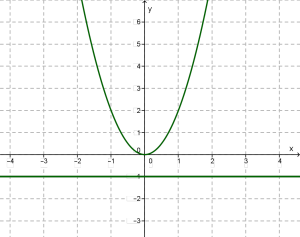
Ուրեմն՝ $y=x^2$ ֆունկցիան սահմանափակ է ներքևից:

Տեսնում ենք, որ պարաբոլն անվերջ շարունակվում է դեպի վեր: Ուրեմն, $y=x^2$ ֆունկցիան վերևից սահմանափակ չէ: