Քառակուսային անհավասարում — դաս։ Հանրահաշիվ, 9-րդ դասարան.

Քառակուսային անհավասարման ընդհանուր տեսքը հետևյալն է ՝

a x^{2} + bx + c > 0 (< 0, \leq 0, \geq 0), որտեղ a \neq 0

Քառակուսային անհավասարման լուծումների բազմությունը հեշտ կարելի է պարզել՝ մոտավորապես կառուցելով նրա գրաֆիկը (պարաբոլը):

Քառակուսային անհավասարման լուծման քայլերը:

1. Լուծելով

a x^{2} + bx + c = 0

քառակուսային հավասարումը, գտնում ենք պարաբոլի հատման կետերը \(x\)-երի առանցքի հետ:

Հիշենք քառակուսային հավասարման արմատների բանաձևերը:

$\begin{array}{l} D = b^{2} - 4 ac \\ x_{1} = \frac{- b + \sqrt{D}}{2 a}, x_{2} = \frac{- b - \sqrt{D}}{2 a} \end{array}$

Եթե \(D > 0\), ապա հավասարումն ունի երկու իրարից տարբեր արմատ: Պարաբոլը հատում է \(x\)-երի առանցքը երկու կետերում: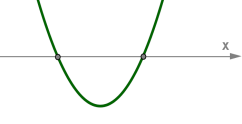
Եթե \(D = 0\), ապա հավասարումն ունի մեկ արմատ: Պարաբոլի գագաթը գտնվում է \(x\)-երի առանցքի վրա: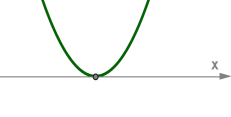
Եթե \(D < 0\), ապա հավասարումը արմատ չունի: Պարաբոլը չի հատում \(x\)-երի առանցքը: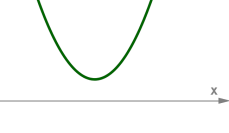

2. Հաշվի առնելով արմատների քանակը և \(a\) գործակցի նշանը` պարաբոլը մոտավորապես գծվում է:

Ուշադրություն

Եթե \(a > 0\), ապա պարաբոլի ճյուղերը ուղղված են դեպի վերև, իսկ եթե \(a < 0\), ապա պարաբոլի ճյուղերը ուղղված են դեպի ներքև:

Խորհուրդ

Եթե ուզում ես, որ պարաբոլի ճյուղերը ուղղված լինեն դեպի վերև, ապա \(a < 0\) դեպքում անհավասարման երկու մասերը բազմապատկիր (\(-1\))-ով:

Չմոռանաս, որ այդ դեպքում փոխվում է նաև անհավասարման նշանը:

3. Անհավասարման նշանից կախված՝ ընտրում ենք հատման կետերի նշանակումը:

Ընտրում ենք

•

նշանակումը, եթե անհավասարման նշանը ոչ խիստ է՝ «

\leq

» կամ «

\geq

»

Ընտրում ենք

о

նշանակումը, եթե անհավասարման նշանը խիստ է՝ «\(<\)» կամ «\(<\)»

4. Կոորդինատային առանցքի վրա նշում ենք ճիշտ միջակայքը:

5. Գրում ենք պատասխանը:

Օրինակ

Լուծենք

- 2 x^{2} + 4 x - 5 \leq 0

քառակուսային անհավասարումը:

Լուծում

\begin{array}{l} - 2 x^{2} + 4 x - 5 \leq 0 | \cdot (- 1) \\ 2 x^{2} - 4 x + 5 \geq 0 \\ D = 16 - 4 \cdot 2 \cdot 5 = - 24 \\ պարաբոլը չի հատում Ox առանցքը \end{array}

Գծագրից տեսնում ենք, որ ֆունկցիան դրական է ցանկացած \(x\)-ի համար:

Պատասխան՝

x \in (- \infty; + \infty) կամ x \in R

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ