Ուղղանկյունանիստ, խորանարդ

Մինչև հիմա մենք ուսումնասիրում էինք երկրաչափության այն բաժինը, որը կոչվում է հարթաչափություն: Այդ բաժինը հարթ պատկերների (պատկերներ, որոնք ամբողջովին ընկած են որևէ հարթության մեջ) և նրանց հատկությունների վերաբերյալ էր: Սակայն մեզ շրջապատող առարկաները հիմնականում հարթ չեն: Ցանկացած իրական առարկա զբաղեցնում է տարածության մի մասը:
Երկրաչափության այն բաժինը, որը ուսումնասիրում է պատկերների հատկությունները տարածության մեջ, կոչվում է տարածաչափություն:
Տարածաչափության պարզագույն պատկերները կետերն են, ուղիղները և հարթությունները: Դրանցից են բաղկացած տարածաչափական մարմինները և նրանց մակերևույթները:
Եթե տարածական մարմնի մակերևույթը կազմված է միայն բազմանկյուններից, ապա մարմինը կոչվում է բազմանիստ:
Բազմանկյունները, որոնցից կազմված է բազմանիստի մակերևույթը, կոչվում են նիստեր: Նիստերի կողմերը կոչվում են բազմանիստի կողեր: Կողերի ծայրակետերը կոչվում են բազմանիստի գագաթներ:
Բազմանիստի նույն նիստի վրա չգտնվող երկու գագաթները միացնող հատվածը կոչվում է բազմանիստի անկյունագիծ:
Զուգահեռանիստ
Զուգահեռանիստ կոչվում է այն բազմանիստը, որի բոլոր բազմանկյունները զուգահեռագծեր են:
Զուգահեռանիստի բոլոր նիստերը զուգահեռագծեր են:
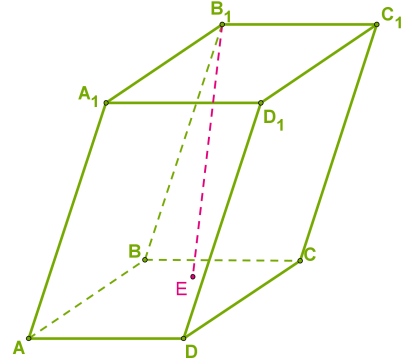
Եթե զուգահեռանիստի երկու նիստեր չունեն ընդհանուր կողեր (ոչ էլ ընդհանուր գագաթներ), ապա դրանք կոչվում են հանդիպակաց նիստեր:
Հանդիպակաց նիստերից երկուսը, օրինակ՝ -ն և -ը կոչվում են զուգահեռանիստի հիմքեր, իսկ մյուսները՝ կողմնային նիստեր:
Ուշադրություն
Զուգահեռանիստն ունի 2 հիմք, 4 կողմնային նիստ, 12 կող և 8 գագաթ:
Ուղղանկյունանիստ և խորանարդ
Այն զուգահեռանիստը, որի բոլոր նիստերը ուղղանկյուններ են, կոչվում է ուղղանկյունանիստ:
Ուղղանկյունանիստն ունի 6 նիստ, 12 կող, 8 գագաթ և 4 անկյունագիծ:
Ուղղանկյունանիստի բոլոր չորս անկյունագծերը հավասար են:
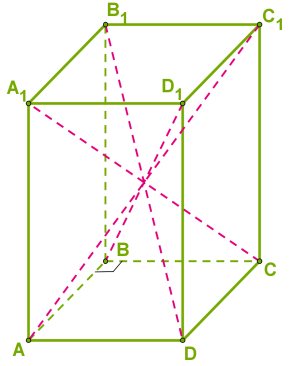
Այն ուղղանկյունանիստը, որի բոլոր կողերը հավասար են, կոչվում է խորանարդ:
Ուշադրություն
Այսպիսով, խորանարդի բոլոր նիստերը քառակուսիներ են:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:


