2. y = arccos x ֆունկցիայի հատկություններն ու գրաֆիկը

 \(x\) թվի արկկոսինուս կոչվում է 0;π հատվածի այն թիվը, որի կոսինուսը \(x\)-ն է:
Հիշենք, որ y=cosx ֆունկցիան 0;π հատվածում խիստ նվազում է, հետևաբար, հակադարձելի է:
 
Յուրաքանչյուր \(x\) թվին −1;1-ից համապատասխանեցնելով y=arccosx թիվը, ստանում ենք −1;1 հատվածում որոշված ֆունկցիա՝ y=arccosx
y=arccosx-ը y=cosx-ի հակադարձ ֆունկցիան է, որտեղ x∈0;π
Հետևաբար,
 
ա) կամայական x∈−1;1 թվի համար cosarccosx=x,
բ) կամայական x∈0;π թվի համար arccoscosx=x:
 
y=arccosx-ի գրաֆիկը համաչափ է y=cosx-ի գրաֆիկին y=x առանցքի նկատմամբ:
 
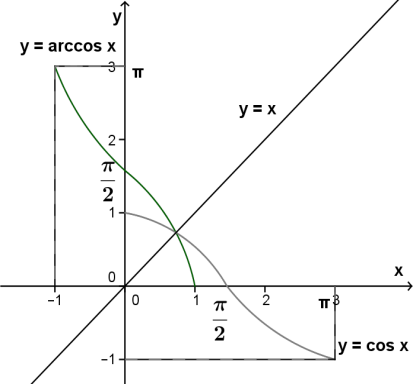
12.png
 
y=arccosx ֆունկցիայի հատկությունները
1. y=arccosx ֆունկցիայի որոշման տիրույթը −1;1 հատվածն է:  
 
2. y=arccosx ֆունկցիայի արժեքների բազմությունը 0;π հատվածն է:
 
3. y=arccosx ֆունկցիան նվազող է:
 
4. arccos−x=π−arccosx
Աղբյուրները
Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:
Նախորդ տեսություն
Վերադառնալ թեմային
Հաջորդ առաջադրանքը
Copyright © 2024 ԻմԴպրոց ՍՊԸ