Ռացիոնալ արտահայտությունների պարզեցումը

Ռացիոնալ արտահայտություն կոչվում է այն արտահայտությունը, որում մի քանի հանրահաշվական կոտորակներ միացված են թվաբանական գործողությունների նշաններով:

Օրինակ

Ռացիոնալ են հետևյալ արտահայտությունները՝

\frac{x + 3}{{(x + 2)}^{2}} + 2 x, \frac{a}{2} + 3 \cdot \frac{a (2 a + 3)}{a^{2} + 2 a + 11}, \frac{x^{2} + 1}{3 x - 1} : \frac{2 x}{3 + 5 x} :

Մենք արդեն դիտարկել ենք թվաբանական գործողություններ հանրահաշվական կոտորակների հետ, դրանց բոլորի արդյունքում, ըստ բերված սահմանման, առաջանում են ռացիոնալ արտահայտություններ: Սակայն մեր դիտարկումներում մասնակցում էր միայն մեկ գործողություն (գումարում, հանում, բազմապատկում, բաժանում կամ աստիճան բարձրացում):

Հիմա կդիտարկենք և կպարզեցնենք ավելի բարդ ռացիոնալ արտահայտություններ, որոնցում կատարվում են մի քանի գործողություններ հանրահաշվական կոտորակների հետ:

\frac{a + 1}{7 c} \cdot \frac{7 + 6 c}{x} \div \frac{3 (a + 1)}{x^{2}}

— կոտորակների բազմապատկում և բաժանում

\frac{a^{2} - y^{2}}{c^{2} - d^{2}} \cdot \frac{c - d}{a - y} - \frac{y}{d + c}

— կոտորակների բազմապատկում և հանում

{(\frac{m + 1}{m})}^{2} + \frac{3 - m + 15}{m (m + 2)}

— կոտորակերի աստիճան բարձրացում և գումարում

Որպեսզի այսպիսի արտահայտությունները ճիշտ պարզեցնել, պետք է՝

պահպանել գործողությունների հերթականությունը,
պահպանել այդ գործողությունների կատարման կանոնները,
հիշել, որ բոլոր գործողությունները կատարվում են միայն այն արժեքների համար, որոնց դեպքում կոտորակներն իմաստ ունեն:

Օրինակ

Կատարենք գործողությունները՝

\frac{x - y}{6 y} \div \frac{x^{2} - y^{2}}{y} \cdot \frac{x^{2} + 2 xy + y^{2}}{x}

Լուծում: Այս առաջադրանքը կարելի է կատարել երկու եղանակներով:

Առաջին եղանակ:

Պարզեցումը կատարվում է երկու գործողություններով՝ սկզբում կատարվում է բաժանումը, ապա բազմապատկումը: Յուրաքանչյուր գործողության ժամանակ կոտորակների համարիչներն ու հայտարարները պետք է վերլուծել արտադրիչների:

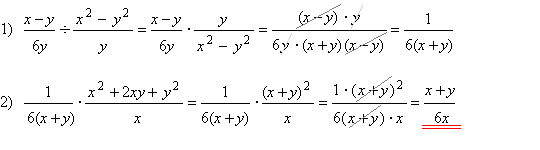
Երկրորդ եղանակ:

Բաժանումը ու բազմապատկումը կատարվում է միաժամանակ: Բոլոր կոտորակների համարիչներն ու հայտարարները գրվում են մեկ կոտորակում, ապա կատարվում է արտադրիչների վերլուծում և կրճատում:

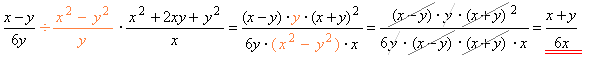
Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:

Վերադառնալ թեմային

Հաջորդ տեսությունը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Ռացիոնալ արտահայտությունների պարզեցումը

Տեսություն