ֆունկցիայի հատկությունները \(k > 0\) դեպքում
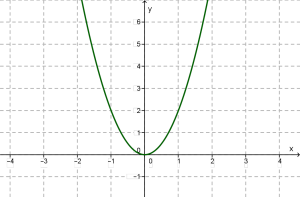
1. ֆունկցիան որոշված է \(x\) -ի ցանկացած արժեքի համար, այսինքն՝ ֆունկցիայի որոշման տիրույթը ամբողջ թվային առանցքն է:
2. \(y = 0\), եթե \(x = 0\) և \(у > 0\), եթե : Դա երևում է գրաֆիկից:
3. ֆունկցիան աճում է, եթե և նվազում է, եթե
4. Եթե \(x\)-ը անսահման տարածվում է դեպի աջ կամ դեպի ձախ (դրական կամ բացասական մնալով), ապա ֆունկցիայի արժեքները դրական մնալով՝ անսահման մեծանում են:
5. ֆունկցիայի փոքրագույն արժեքը զրոն է՝ , ֆունկցիան այդ արժեքը ընդունում է \(х = 0\) դեպքում: Մեծագույն արժեք ֆունկցիան չունի:
6. ֆունկցիան անընդհատ է, քանի որ նրա գրաֆիկը անընդհատ կոր է, որը կարելի է գծել՝ առանց մատիտը թղթից կտրելու:
7. \((k > 0)\) ֆունկցիան սահմանափակ է ներքևից և սահմանափակ չէ վերևից:
8. \((k>0)\) ֆունկցիայի արժեքների բազմությունը ճառագայթն է:
ֆունկցիայի հատկությունները \(k < 0\) դեպքում
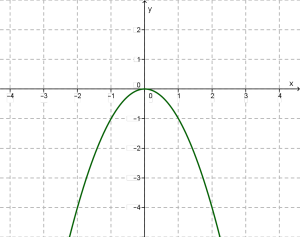
1. ֆունկցիայի որոշման տիրույթը ամբողջ թվային առանցքն է:
2. \(y = 0\), եթե \(x = 0\) և \(у < 0\), եթե :
3. ֆունկցիան նվազում է, եթե և աճում է, եթե
4. Եթե \(x\)-ը անսահման տարածվում է դեպի աջ կամ դեպի ձախ (դրական կամ բացասական մնալով), ապա ֆունկցիայի արժեքները բացասական մնալով՝ անսահման մեծանում են մոդուլով:
5. ֆունկցիայի մեծագույն արժեքը զրոն է՝ , ֆունկցիան այդ արժեքը ընդունում է \(х = 0\) դեպքում: Ֆունկցիան փոքրագույն արժեք չունի:
6. ֆունկցիան անընդհատ է, նրա գրաֆիկը անընդհատ կոր է, որը կարելի է գծել՝ առանց մատիտը թղթից կտրելու:
7. \((k < 0)\) ֆունկցիան սահմանափակ է վերևից և սահմանափակ չէ ներքևից:
8. \((k<0)\) ֆունկցիայի արժեքների բազմությունը ճառագայթն է:
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013:


