
















Զուգահեռ ուղիղների հատկությունները, զուգահեռ ուղիղների աքսիոմը
Հայտանիշները, որոնք մենք դիտարկեցինք տեսության առաջին մասում, և հատկությունները, որոնք դիտարկելու ենք հիմա, ապացուցվում են տարբեր եղանակներով:
Հայտանիշը որոշակի փաստ է, որի օգնությամբ մենք ապացուցում ենք մեզ հետաքրքրող առարկայի վերաբերյալ պնդումը:
Եթե երկու ուղիղներ երրորդով հատելիս խաչադիր անկյունները հավասար են, ապա ուղիղները զուգահեռ են:
Հատկությունն այն է, երբ մենք վստահ ենք, որ առարկայի վերաբերյալ պնդումը ճիշտ է, մենք այն ձևակերպում ենք որպես դրա հատկություն:
Եթե երկու ուղիղներ զուգահեռ են, ապա երրորդ ուղղով հատվելիս խաչադիր անկյունները հավասար են:
Աքսիոմն այնպիսի ճշմարտություն է, որը չի ապացուցվում: Յուրաքանչյուր գիտություն ունի իր աքսիոմները, որոնց վրա են հիմնվում բոլոր հետագա պնդումներն ու ապացույցները:
Զուգահեռ ուղիղների աքսիոմը.
Տրված ուղղի վրա չգտնվող կետով անցնում է այդ ուղղին զուգահեռ միայն մեկ ուղիղ:
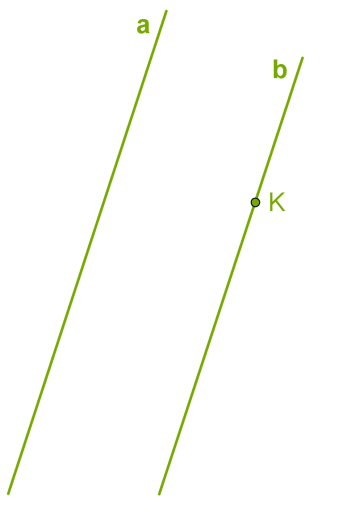
Զուգահեռ ուղիղների այլ հատկություններ.
1. Եթե երկու ուղիղներ զուգահեռ են երրորդ ուղղին, ապա դրանք զուգահեռ են:
2. Եթե ուղիղը հատում է զուգահեռ ուղիղներից մեկը, ապա այն հատում է նաև երկրորդը:
Ի տարբերություն աքսիոմի՝ այս հատկությունները պետք է ապացուցել:
Ապացուցենք \(1\)-ին հատկությունը:
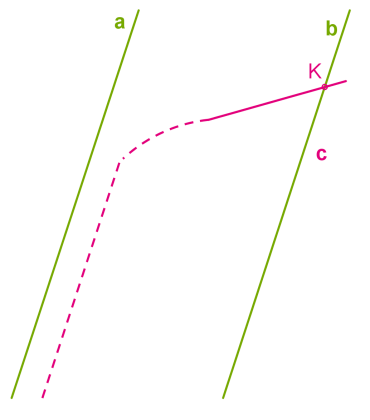
Տրված են \(a\) և \(b\) զուգահեռ ուղիղները: Ապացուցենք, որ եթե \(c\) ուղիղը զուգահեռ է \(a\) ուղղին, ապա այն զուգահեռ է նաև \(b\) ուղղին:
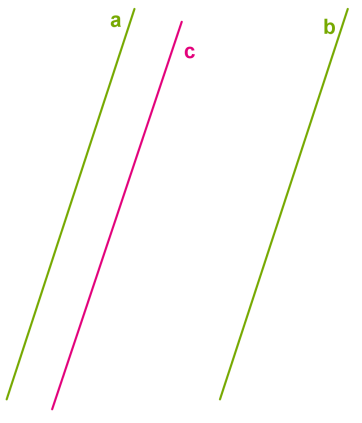
Կատարենք հակասող ենթադրություն:
Դիցուք, \(c\) ուղիղը զուգահեռ է ուղիղներից մեկին, օրինակ՝ \(a\)-ին և հատում է \(b\) ուղիղը որոշ \(K\) կետում:
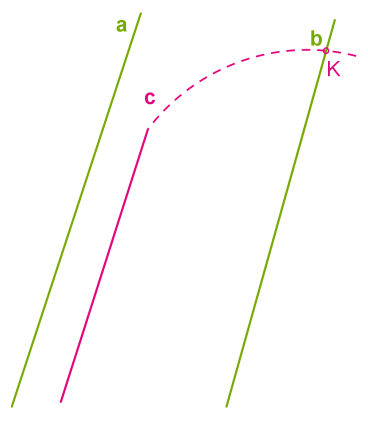
Ստանում ենք հակասություն զուգահեռ ուղիղների աքսիոմին: Մենք ունենք իրավիճակ, երբ կետով անցնում են երկու հատվող ուղիղներ, որոնք զուգահեռ են միևնույն \(a\) ուղղին: Այդպիսի բան լինել չի կարող, ուրեմն \(b\) և \(c\) ուղիղները չեն կարող հատվել:
Մենք ապացուցեցինք, որ եթե զուգահեռ ուղիղներից մեկը զուգահեռ է երրորդ ուղղին, ապա երկրորդը ևս զուգահեռ է դրան:
Փորձիր ինքնուրույն ապացուցել \(2\)-րդ հատկությունը:
Եթե \(c\) ուղիղը հատում է զուգահեռ ուղիղներից մեկը՝ \(a\)-ն, ապա այն հատում է նաև մյուսը՝ \(b\)-ն:
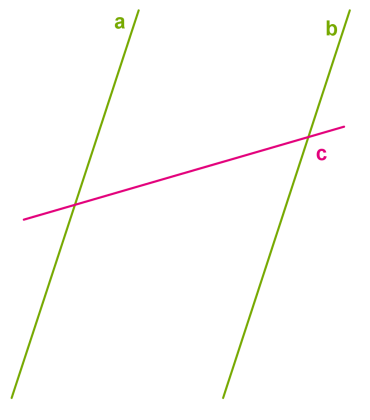
Այդ նույն մեթոդով, հակադարձ պնդումով, փորձիր պատկերացնել, որ հնարավոր է այնպիսի իրավիճակ, երբ ուղիղը հատում է զուգահեռ ուղիղներից մեկը, բայց չի հատում մյուսը:
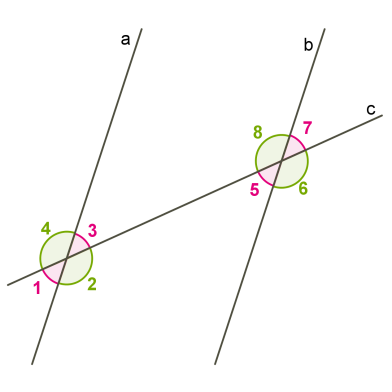
Առաջին մասում մենք արդեն դիտարկել ենք անկյունները, որոնք առաջանում են, երբ ուղիղը հատում է զուգահեռ ուղիղները:
Եթե ուղիղը հատում է զուգահեռ ուղիղները, ապա՝
- խաչադիր անկյունները հավասար են,
- համապատասխան անկյունները հավասար են,
- միակողմանի անկյունների գումարը հավասար է \(180°\)-ի:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 7-րդ դասարան, Երևան, "Զանգակ 97", 2011: