Ուղիղ պրիզմայի և կանոնավոր բուրգի մակերևույթների մակերեսները

Ուղիղ պրիզմայի մակերևույթի մակերեսի հաշվման հիմնական բանաձևերը

Այս նկարներում ցուցադրված են ուղիղ պրիզմաներ՝ առաջինը եռանկյուն, իսկ երկրորդը՝ քառանկյուն:

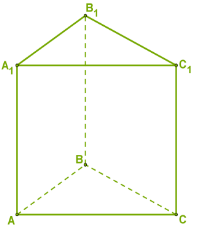
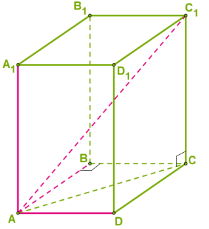
Ուղիղ պրիզմայի բոլոր կողմնային նիստերը ուղղանկյուններ են, հետևաբար, նրա կողմնային մակերևույթի մակերեսը հավասար է այդ ուղղանկյունների մակերեսների գումարին:

1. Ուղիղ պրիզմայի կողմնային մակերևույթի մակերեսը հաշվում են

S_{կողմն} = P_{հիմք} \cdot H

բանաձևով, որտեղ \(H\)-ը կողմնային կողն է, իսկ

P_{հիմք}

-ը՝ հիմքի պարագիծը:

Այսպիսով, ուղիղ պրիզմայի կողմնային մակերևույթի մակերեսը հավասար է նրա հիմքի պարագծի և կողմնային կողի արտադրյալին:

Թեք պրիզմաների համար յուրաքանչյուր նիստի մակերեսը պետք է հաշվել առանձին:

2. Պրիզմայի լրիվ մակերևույթի մակերեսը հաշվում են

S_{լրիվ} = 2 \cdot S_{հիմք} + S_{կողմն}

բանաձևով:

Պրիզմայի լրիվ մակերևույթի մակերեսը հավասար է նրա երկու հիմքերի և բոլոր կողմնային նիստերի մակերեսների գումարին:

Այս բանաձևը ճիշտ է բոլոր պրիզմաների համար:

Բերված բանաձևերը ճիշտ են պրիզմաների բոլոր տարատեսակների համար, մասնավորապես՝ զուգահեռանիստերի, ուղղանկյունանիստերի և խորանարդների համար:

Կանոնավոր բուրգի մակերևույթի մակերեսի հաշվման հիմնական բանաձևերը

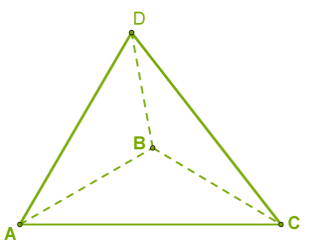
Այս նկարներում ցուցադրված են կանոնավոր բուրգեր՝ առաջինը քառանկյուն, իսկ երկրորդը՝ եռանկյուն:

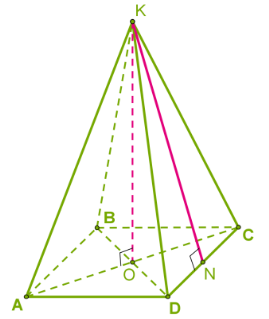
Առաջին նկարում ցուցադրված քառանկյուն բուրգի \(DKC\) նիստում \(K\) գագաթից տարված է \(KN\) բարձրությունը \(DC\) կողին:

Բուրգի կողմնային նիստի բարձրությունը, որը տարված է բուրգի գագաթից դեպի հիմքի կողը, կոչվում է հարթագիծ:

Կանոնավոր բուրգի բոլոր կողմնային նիստերը հավասարասրուն եռանկյուններ են, հետևաբար, նրա կողմնային մակերևույթի մակերեսը հավասար է այդ եռանկյունների մակերեսների գումարին:

1. Կանոնավոր բուրգի կողմնային մակերևույթի մակերեսը հաշվում են