3. Չափումների ճշգրտությունն ու սխալը

 

 

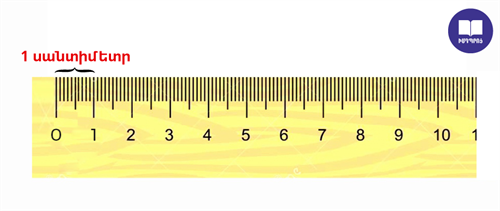
Որպես օրինակ դիտարկենք չորսուի երկարության չափումը սանտիմետրանոց բաժանումներ ունեցող քանոնով:

 

 

Որոշենք քանոնի բաժանման արժեքը: Այն հավասար է \(1\) սմ-ի: Եթե չորսուի ձախ եզրը համատեղենք \(0\)-ական նրբագծի հետ, ապա աջ եզրը կտեղակայվի \(9\) և \(10\) նրբագծերի միջև, սակայն ավելի մոտ \(10\) –ին: Այդ դեպքում այս երկու արժեքներից ո՞րը կհամապատասխանի չորսուի երկարությանը: Ակնհայտ է այն, որը մոտ է իրական արժեքին՝ \(10\) սմ: Ընդունելով չորսուի երկարությունը \(10\) սմ-ի հավասար, մենք թույլ կտանք անճշտություն, քանի որ չորսուն փոքր ինչ կարճ է \(10\) սմ-ից:

Մեր նկարագրած դեպքում չափման սխալը չի գերազանցում \(1\) սմ-ի: Եթե չափման այդ ճշգրտությունը մեզ չի բավարարում, ապա չափումը կարող ենք կատարել ավելի մեծ ճշգրտությամբ: Պետք է վերցնել միլիմետրանոց բաժանումներով չափաքանոն, որի չափման արժեքը \(1\) մմ է: Այս դեպքում քանոնի երկարությունը \(9,8\) սմ է:

Այս օրինակից հետևում է, որ չափումների ճշգրտությունը կախված է սարքի սանդղակի բաժանման արժեքից:

Չափման ճշգրտությունը կախված է նաև չափիչ սարքի ճիշտ օգտագործումից, աչքերի դիրքից, երբ հաշվում են չափիչ սարքով:

 

Չափիչ սարքերի որոշակի թերությունների և մեր զգայարանների զարգացման որոշ թերությունների պատճառով, ցանկացած չափման ժամանակ մենք ստանում ենք մոտավոր արժեքներ՝ չափվող մեծության արժեքից փոքր կամ մեծ:

 

Չափման սխալով մեծության ներկայացման գրառման ժամանակ պետք է օգտվել $A=a\pm \mathrm{\Delta }a$ բանաձևից, որտեղ \(A\)՝ չափվող մեծությունն է, \(a\)՝ չափման արդյունքն է, $\mathrm{\Delta }a$-ն չափման սխալն է ( $\mathrm{\Delta }$՝ հունական այբուբենի տառ է «դելտա»):