
















Երկու ուղիղների փոխդասավորությունը
Հարթաչափության դասընթացից գիտենք, որ հարթության մեջ երկու ուղիղները լինում են հատվող (ունեն ընդհանուր կետ) կամ՝ զուգահեռ (ընդհանուր կետեր չունեն):
Նույն հարթության մեջ գտնվող չհատվող ուղիղները կոչվում են զուգահեռ:
Տարածության մեջ երկու ուղիղները կարող են չհատվել և չլինել զուգահեռ:

Երկաթգիծը չի հատում կամուրջը և զուգահեռ չէ դրան:

Կամուրջի ամրաձողերը:

Տանիքի հորիզոնական գծերը և պատերի ուղղահայաց գծերը:
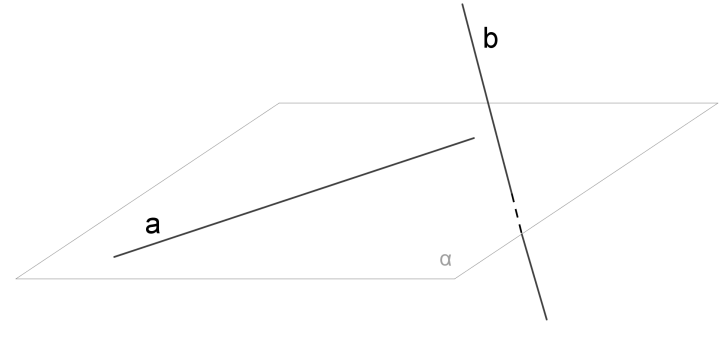
Մի հարթության մեջ չգտնվող ուղիղները կոչվում են խաչվող:
Թեորեմ (խաչվող ուղիղների հայտանիշը)
Եթե երկու ուղիղներից մեկը գտնվում է որևէ հարթության մեջ, իսկ մյուսը հատում է այդ հարթությունը առաջին ուղղին չպատկանող կետում, ապա այդ ուղիղները խաչվում են:
Ապացույց:
Դիտարկենք \(α\) հարթության մեջ գտնվող \(AB\) ուղիղը, և \(CD\) ուղիղը, որը հարթությունը հատում է \(AB\)-ին չպատկանող \(D\) կետում:
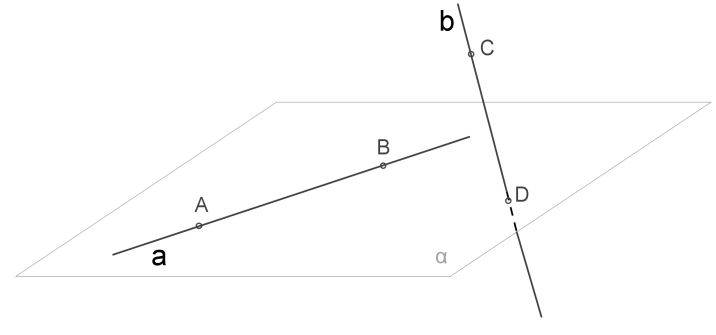
1. Կատարենք հակասող ենթադրություն, որ \(AB\) և \(CD\) ուղիղները ընկած են միևնույն հարթության մեջ:
2. Այդ հարթությունը պարունակում է \(AB\) ուղիղն ու \(D\) կետը, հետևաբար այդ հարթությունը համընկնում է \(α\) հարթության հետ:
3. Սա հակասում է թեորեմի այն պայմանին, որ \(CD\) ուղիղը չի գտնվում \(α\) հարթության մեջ՝ այլ հատում է այն:
Թեորեմն ապացուցված է:
2. Այդ հարթությունը պարունակում է \(AB\) ուղիղն ու \(D\) կետը, հետևաբար այդ հարթությունը համընկնում է \(α\) հարթության հետ:
3. Սա հակասում է թեորեմի այն պայմանին, որ \(CD\) ուղիղը չի գտնվում \(α\) հարթության մեջ՝ այլ հատում է այն:
Թեորեմն ապացուցված է:
Գոյություն ունեն տարածության մեջ երկու ուղիղների փոխդասավորության մի քանի դեպքեր:
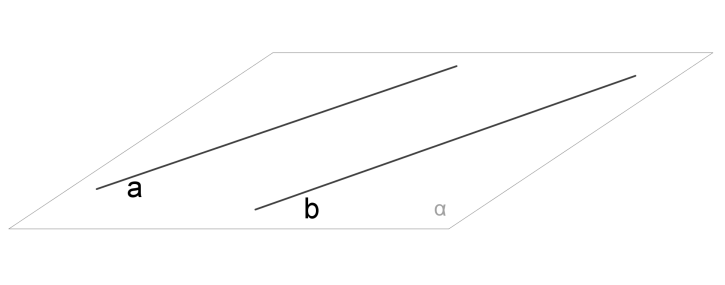
1. Զուգահեռ ուղիղներ
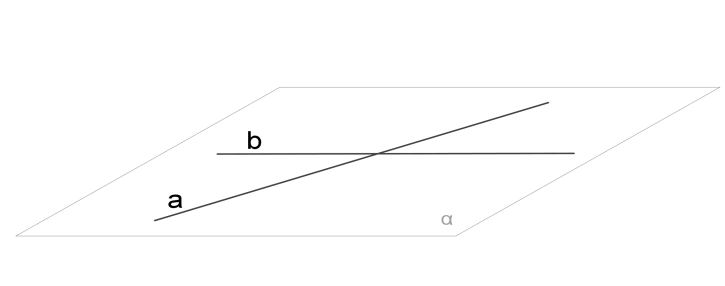
2. Հատվող ուղիղներ
3. Խաչվող ուղիղներ

Թեորեմ
Խաչվող ուղիղներից յուրաքանչյուրով կարելի է տանել հարթություն, որը զուգահեռ է երկրորդ ուղղին և այն էլ՝ մեկը:
Ապացույց:
Դիտարկենք \(AB\) և \(CD\) խաչվող ուղիղները:
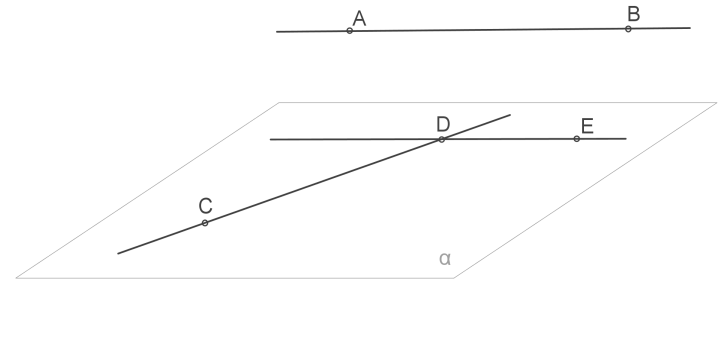
1. \(D\) կետով կարելի է տանել \(AB\)-ին զուգահեռ \(DE\) ուղիղը:
2. \(CD\) և \(DE\) հատվող ուղիղներով կարելի է տանել \(α\) հարթությունը:
3. Քանի որ \(АB\)-ն չի գտնվում \(α\) հարթության մեջ և զուգահեռ է \(DE\)-ին, ապա այն զուգահեռ է \(α\) հարթությանը:
2. \(CD\) և \(DE\) հատվող ուղիղներով կարելի է տանել \(α\) հարթությունը:
3. Քանի որ \(АB\)-ն չի գտնվում \(α\) հարթության մեջ և զուգահեռ է \(DE\)-ին, ապա այն զուգահեռ է \(α\) հարթությանը:
4. Այդ հարթությունը միակն է, քանի որ \(CD\)-ով անցնող ցանկացած ուրիշ ուղիղ կհատվի \(DE\)-ի և նրան զուգահեռ \(AB\)-ի հետ:
Թեորեմն ապացուցված է:
Թեորեմն ապացուցված է:
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009