Արտագծյալ և ներգծյալ շրջանագծեր — դաս։ Երկրաչափություն, 8-րդ դասարան.

Արտագծյալ շրջանագիծ

Եթե բազմանկյան բոլոր գագաթները գտնվում են շրջանագծի վրա, ապա շրջանագիծը կոչվում է այդ բազմանկյան արտագծյալ շրջանագիծ:

Շրջանագծի կենտրոնը հավասարահեռ է բազմանկյան բոլոր գագաթներից, հետևաբար այն գտնվում է բազմանկյան կողմերի միջնուղղահայացների հատման կետում:

Ոչ բոլոր բազմանկյուններն ունեն արտագծյալ շրջանագիծ՝ հաճախ բազմանկյան համար գոյություն չի ունենում այնպիսի շրջանագիծ, որը կանցնի բազմանկյան բոլոր գագաթներով:

Քանի որ եռանկյան կողմերի միջնուղղահայացները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի արտագծյալ շրջանագիծ:

Սուրանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներսում (տես ներքևի նկարը):

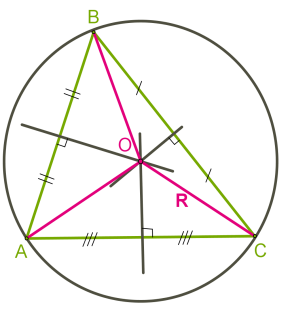
Ուղղանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյան ներքնաձիգի վրա (տես ներքևի նկարը):

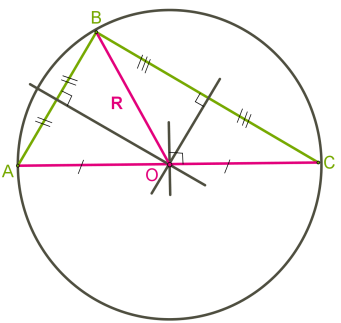
Բութանկյուն եռանկյան դեպքում, արտագծյալ շրջանագծի կենտրոնը գտնվում է եռանկյունից դուրս (տես ներքևի նկարը):

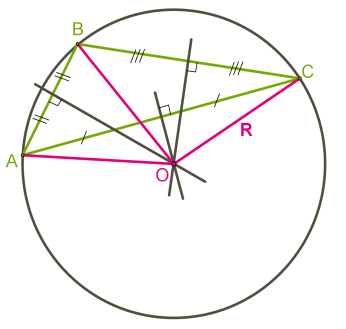
Ներգծյալ շրջանագիծ

Եթե բազմանկյան բոլոր կողմերը շոշափում են շրջանագիծը, ապա շրջանագիծը կոչվում է այդ բազմանկյան ներգծյալ շրջանագիծ:

Ներգծված շրջանագծի կենտրոնը պետք է հավասարահեռ լինի բազմանկյան կողմերից, այսինքն լինի կիսորդների հատման կետում:

Քանի որ եռանկյան անկյունների կիսորդները հատվում են նույն կետում, ապա ցանկացած եռանկյուն ունի ներգծյալ շրջանագիծ:

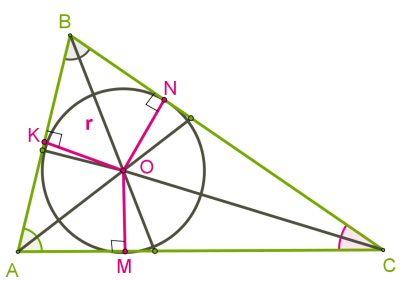
Քանի որ, ցանկացած եռանկյան անկյունների կիսորդները հատվում են եռանկյան ներսում, ապա ներգծյալ շրջանագծի կենտրոնը միշտ գտնվում է եռանկյան ներսում:

Բանաձևեր

Հավասարակողմ եռանկյուն

Հավասարակողմ եռանկյան կողմերի միջնուղղահայացները և անկյունների կիսորդները հատվում են միևնույն կետում:

Ուշադրություն

Հետևաբար, հավասարակողմ եռանկյան արտագծյալ և ներգծյալ շրջանագծերի կենտրոնները համընկնում են:

Արտագծյալ շրջանագծի շառավիղը

R = \frac{2}{3} h

կամ

R = \frac{a \sqrt{3}}{3}

, որտեղ \(h\) -ը եռանկյան բարձրությունն է, իսկ \(a\) -ն՝ կողմը:

Ներգծյալ շրջանագծի շառավիղը

r = \frac{1}{3} h

կամ

r = \frac{a \sqrt{3}}{6}

որտեղ \(h\) -ը եռանկյան բարձրությունն է, իսկ \(a\) -ն՝ կողմը:

Հավասարակողմ եռանկյան բարձրությունը և կողմը կապված են հետևյալ բանաձևով՝

h = \frac{a \sqrt{3}}{2}

Ուղղանկյուն եռանկյուն

Արտագծյալ շրջանագծի շառավիղը

R = \frac{1}{2} c

, որտեղ \(c\) -ն ներքնաձիգն է:

Ներգծյալ շրջանագծի շառավիղը

r = \frac{S_{Δ}}{p}

, որտեղ \(p\) -ն կիսապարագիծն է:

Կամայական եռանկյուն

Արտագծյալ շրջանագծի շառավիղը

R = \frac{a \cdot b \cdot c}{4 \cdot S_{Δ}}

Ներգծյալ շրջանագծի շառավիղը

r = \frac{S_{Δ}}{p}

, որտեղ \(p\) -ն կիսապարագիծն է:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007

Վերադառնալ թեմային

Հաջորդ տեսությունը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Արտագծյալ և ներգծյալ շրջանագծեր

Տեսություն