
















Բերման բանաձևեր
Դիտարկենք \(AOX\) եռանկյան երկու սուր անկյունները: Դրանց գումարը հավասար է
Անկյուններից մեկը նշանակենք -ով, մյուսը կլինի`
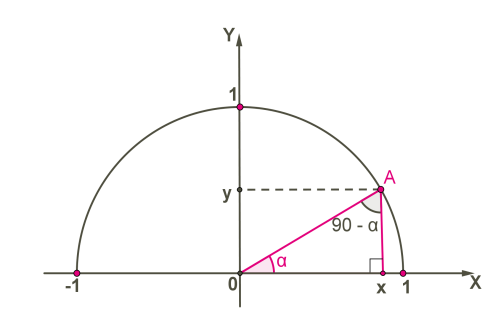
Քանի որ , ապա
Համոզվում ենք, որ տեղի ունեն հետևյալ հավասարությունները՝
Դիտարկենք բութ անկյունը, և այն արտահայտենք -ով:
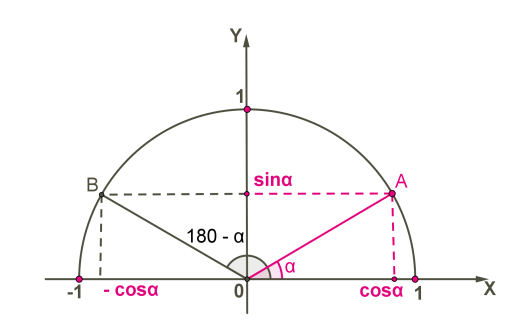

Տեղի ունեն հետևյալ հավասարությունները՝
Ստացված բանաձևերը կոչվում են բերման բանաձևեր՝
Սինուսի և կոսինուսի համար բերման բանաձևերի միջոցով ստանում ենք բերման բանաձևեր տանգենսի և կոտանգենսի համար:
Օրինակ՝ եթե , ապա՝
եթե , ապա՝
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013