Ուղղի հավասարումը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Ուղղի հավասարումը

Տրված ուղղի հավասարումը դուրս բերելու համար, այդ ուղիղը տանենք որպես տրված ծայրակետերով որևէ հատվածի միջնուղղահայաց:

Օգտվենք միջնուղղահայացի հիմնական հատկությունից:

Միջնուղղահայացի բոլոր կետերը հավասարահեռ են հատվածի ծայրակետերից:

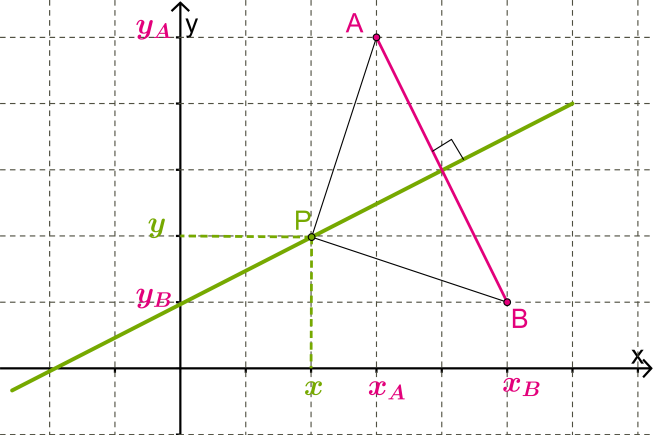
Հատվածի ծայրակետերը

A (x_{A}; y_{A})

B (x_{B}; y_{B})

կետերն են: Միջնուղղահայացի ցանկացած

P (x; y)

կետի համար

PA = PB

, հետևաբար՝

{PA}^{2} = {PB}^{2}

, և ուրեմն, տեղի ունի հետևյալ հավասարությունը՝

{(x - x_{A})}^{2} + {(y - y_{A})}^{2} = {(x - x_{B})}^{2} + {(y - y_{B})}^{2}

Սա հենց ուղղի հավասարումն է: Կատարելով պարզ ձևափոխություններ՝

\begin{array}{l} x^{2} - 2 \cdot x \cdot x_{A} + {(x_{A})}^{2} + y^{2} - 2 \cdot y \cdot y_{A} + {(y_{A})}^{2} = \\ = x^{2} - 2 \cdot x \cdot x_{B} + {(x_{B})}^{2} + y^{2} - 2 \cdot y \cdot y_{B} + {(y_{B})}^{2} \\ 2 \cdot x \cdot x_{B} - 2 \cdot x \cdot x_{A} + 2 \cdot y \cdot y_{B} - 2 \cdot y \cdot y_{A} + {(x_{A})}^{2} - {(x_{B})}^{2} + {(y_{A})}^{2} - {(y_{B})}^{2} = 0 \\ (2 x_{B} - 2 x_{A}) \cdot x + (2 y_{B} - 2 y_{A}) \cdot y + ({(x_{A})}^{2} - {(x_{B})}^{2} + {(y_{A})}^{2} - {(y_{B})}^{2}) = 0 \end{array}

ուղղի հավասարումը գրում ենք հետևյալ տեսքով՝

\begin{array}{l} ax + by + c = 0 \\ a = 2 (x_{B} - x_{A}) \\ b = 2 (y_{B} - y_{A}) \\ c = {(x_{A})}^{2} - {(x_{B})}^{2} + {(y_{A})}^{2} - {(y_{B})}^{2} \end{array}

Դիտարկենք հատուկ ուղիղներ:

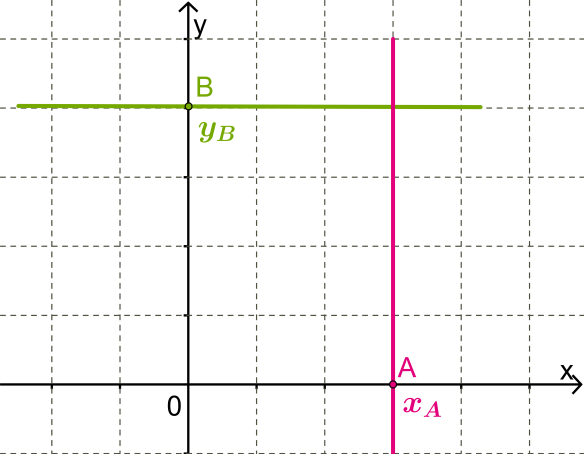
1. Ուղիղը զուգահեռ է \(Oy\) առանցքին և անցնում է

A (x_{A}; 0)

կետով:

Այդ ուղղի հավասարումն է՝

x = x_{A}

: Մասնավորապես,

\(Oy\) առանցքի հավասարումն է՝

x = 0

2. Ուղիղը զուգահեռ է \(Ox\) առանցքին և անցնում է

B (0; y_{B})

կետով:

Այդ ուղղի հավասարումն է՝

y = y_{B}

: Մասնավորապես,

\(Ox\) առանցքի հավասարումն է՝

y = 0

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013

Սխա՞լ ես գտել

1. Ուղղի հավասարումը