
















Մեխանիզմի օգտակար գործողության գործակից (ՕԳԳ)
Օգտակար աշխատանք
Այս կամ այն մեխանիզմը կամ մեքենան մարդիկ օգտագործում են որոշակի աշխատանք կատարելու նպատակով:
Օրինակ, վերելակն օգտագործում են շենքի տարբեր հարկեր բարձրանալու և իջնելու նպատակով: \(m\) զանգվածով մարդուն \(h\) բարձրության բարձրացնելու համար նվազագույնը պետք է կատարել \(Aօգ = mgh\) աշխատանք, որը ծախսվում է նրա վրա ազդող \(mg\) ծանրության ուժը հաղթահարելու համար: Այդ աշխատանքը կատարում է վերելակի շարժիչը:
Այն աշխատանքը, որի կատարման համար ստեղծված է մեխանիզմը կամ մեքենան, կոչվում է օգտակար աշխատանք (\(A\)օգ):
Ծախսված աշխատանք
Ուշադրություն
Եթե բեռը բարձրացնելու համար որևէ մեխանիզմ ենք օգտագործում, ապա բեռի ծանրության ուժից բացի, միշտ էլ հարկ է լինում հաղթահարել նաև մեխանիզմի մասերի ծանրության ուժը, ինչպես նաև այդ մեխանիզմում գործող շփման ուժը։
Օրինակ՝ շարժական ճախարակ օգտագործելիս հարկադրված ենք լինում լրացուցիչ աշխատանք կատարել.
ա) որպեսզի բարձրացնենք ճախարակը և ճոպանը
բ) որպեսզի հաղթահարենք շփման ուժը ճախարակի առանցքում
Մեխանիզմի օգտագործմամբ նպատակին հասնելու համար կատարված ամբողջ աշխատանքը կոչվում է լրիվ աշխատանք (\(A\)լր):
Ուշադրություն
Լրիվ աշխատանքը հավասար է օգտակար և լրացուցիչ աշխատանքների գումարին, ուստի օգտակար աշխատանքը միշտ փոքր է ծախսվածից.
\(Aօգ < Aլր\)
\(Aօգ < Aլր\)
Օգտակար աշխատանքը միշտ լրիվ աշխատանքի որոշ մասն է, որը մարդը կատարում է մեխանիզմների միջոցով։
Օգտակար գործողության գործակից
Այն ֆիզիկական մեծությունը, որը ցույց է տալիս, թե օգտակար աշխատանքը ծախսված աշխատանքի որ մասն է կազմում, կոչվում է մեխանիզմի օգտակար գործողության գործակից (կրճատ՝ ՕԳԳ)։
Մեխանիզմի ՕԳԳ-ն գտնելու համար օգտակար աշխատանքը պետք է բաժանել այն աշխատանքին, որը ծախսվել է տվյալ տեխնիկական սարքն օգտագործելու ժամանակ.
\( ՕԳԳ = (Aօգ )/Aլր \)
\( ՕԳԳ = (Aօգ )/Aլր \)
Օգտակար գործողության գործակիցը հաճախ արտահայտում են տոկոսներով և նշանակում հունական \(η\) (կարդացվում է էտա) տառով.
\(η = (Aօգ )/Aլր · 100%\)
\(η = (Aօգ )/Aլր · 100%\)
Ուշադրություն
Քանի որ \(A\) օգ-ը միշտ փոքր է \(A\) լր-ից, ապա \(ՕԳԳ\)-ն միշտ փոքր է \(1\)-ից (կամ \(100\) %-ից)։
ՕԳԳ-ն բնութագրում է մեխանիզմի աշխատանքի արդյունավետությունը:
Պարզ մեխանիզմների օգտագործմամբ աշխատանքի մեջ շահում ստանալ հնարավոր չէ։ Ավելին, կորուստներից լիովին խուսափել հնարավոր չէ, ուստի իրականում աշխատանքի մեջ միշտ կորցնում ենք:
Պարզ մեխանիզմների օգտագործմամբ աշխատանքի մեջ շահում ստանալ հնարավոր չէ։ Ավելին, կորուստներից լիովին խուսափել հնարավոր չէ, ուստի իրականում աշխատանքի մեջ միշտ կորցնում ենք:
Մեխանիկայի «ոսկե կանոնը»
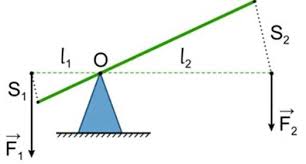
Երբ երկու ուժերի ազդեցության տակ հավասարակշռության մեջ գտնվող լծակը պտտվում է հենարանի շուրջը (տես նկարը), փոքր ուժի կիրառման կետն ավելի մեծ ճանապարհ է անցնում, քան մեծ ուժինը: Չափելով այդ ճանապարհները՝ ստանում ենք, որ դրանք հակադարձ համեմատական են ուժերի մոդուլներին. կամ
Ուշադրություն
Հաշվի առնելով, որ ուժի և ճանապարհի արտադրյալն այդ ուժի կատարած աշխատանքն է, ստանում ենք, որ լծակը հավասարակշռող ուժերի կատարած աշխատանքները միմյանց հավասար են՝
\(=\)
Այսպիսով, մեխանիզմի օգնությամբ քանի անգամ շահում ենք ուժի մեջ, նույնքան անգամ կորցնում ենք ճանապարհի մեջ և հակառակը:
Այս պնդումը կոչվում է մեխանիկայի «ոսկե կանոն»։
Այս պնդումը կոչվում է մեխանիկայի «ոսկե կանոն»։
Աղբյուրները
Գրոմով Ս.Վ., Ռոդինա Ն. Ա., Խմբագրությամբ՝ Ա. Լ. Մամյանի; Դասագիրք հանրակրթական հաստատությունների 7-րդ դասարանի համար - Եր.։ Անտարես, 2013.- 192 էջ։