Կոտորակագծային ֆունկցիա — դաս։ Հանրահաշիվ, 10-րդ դասարան.

Կոտորակագծային կոչվում է

y = \frac{ax + b}{cx + d}

ֆունկցիան, որտեղ \(a)-ն, \(b)-ն, \(c)-ն, \(d)-ն իրական թվեր են:

Համարենք, որ

c \neq 0 և ad \neq bc

, քանի որ \(c = 0\) դեպքում ստանում ենք գծային ֆունկցիա, իսկ \(a·d = b·c\) դեպքում՝ ֆունկցիան հաստատուն է իր որոշման տիրույթում՝

x \neq - \frac{d}{c}

Պարզագույն կոտորակագծային ֆունկցիան մեզ ծանոթ

y = \frac{1}{x}

ֆունկցիան է, որի գրաֆիկը հիպերբոլ է:

Հիշենք

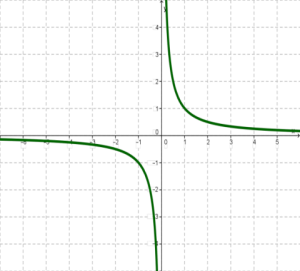
y = \frac{1}{x}

ֆունկցիայի հատկությունները:

1. Ֆունկցիայի որոշման տիրույթը

D = (- \infty; 0) \cup (0; + \infty)

բազմությունն է:

2. Ֆունկցիայի արժեքների բազմությունը

E (y) = (- \infty; 0) \cup (0; + \infty)

բազմությունն է:

3. Եթե \(x > 0\), ապա \(y > 0\): Եթե \(x < 0\), ապա \(y < 0\):

4. Ֆունկցիան նվազում է

(- \infty; 0) և (0; + \infty)

միջակայքերի վրա:

5. Ֆունկցիան ոչ վերևից, ոչ էլ ներքևից սահմանափակ չէ:

6. Ֆունկցիան չունի ոչ մեծագույն, ոչ էլ փոքրագույն արժեքներ:

7. Ֆունկցիան անընդհատ է

(- \infty; 0) և (0; + \infty)

միջակայքերում, իսկ \(x = 0\) կետում խզվում է:

Աղբյուրները

Գ. Գ. Գևորգյան, Ա..Ա. Սահակյան, Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր, 10-րդ դասարան, Տիգրան Մեծ, 2009:

Սխա՞լ ես գտել

1. Կոտորակագծային ֆունկցիա