Հանրահաշվական կոտորակների գումարումն ու հանումը

Հավասար հայտարարներով կոտորակների գումարման և հանման ժամանակ՝ գումարվում կամ հանվում են նրանց համարիչները, իսկ հայտարարները մնում են անփոփոխ:

\frac{3}{15} + \frac{9}{15} = \frac{12}{15} և \frac{6}{7} - \frac{4}{7} = \frac{2}{7}

Նույն կանոնով գումարվում և հանվում են հավասար հայտարարներով հանրահաշվական կոտորակները՝

հանրահաշվական կոտորակների գումարման ժամանակ, համարիչները գումարվում են, իսկ հայտարարները մնում են անփոփոխ՝

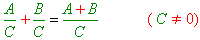
հանրահաշվական կոտորակների հանման ժամանակ, համարիչները հանվում են, իսկ հայտարարները մնում են անփոփոխ՝

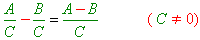
Նույն կանոնով կարելի է գումարել կամ հանել հավասար հայտարարներով մի քանի կոտորակներ՝

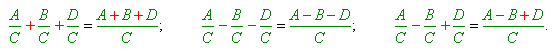
Օրինակ

\begin{array}{l} 1) \frac{x}{x - 1} + \frac{4}{x - 1} = \frac{x + 4}{x - 1} \\ 2) \frac{3 a + 5}{b} + \frac{2 a - 4}{b} = \frac{3 a + 5 + 2 a - 4}{b} = \frac{5 a + 1}{b} \\ 3) \frac{10 m}{m + 3} - \frac{7 m - 9}{m + 3} = \frac{10 m - (7 m - 9)}{m + 3} = \frac{10 m - 7 m + 9}{m + 3} = \frac{3 m + 9}{m + 3} = \frac{3 (m + 3)}{m + 3} = \frac{3}{1} = 3 \end{array}

Դիտողություն: Այս դեպքում կոտորակների որոշման տիրույթները նշելու կարիք չկա: Սակայն պետք է հիշել, որ հանրահաշվական կոտորակների հետ ցանկացած ձևափոխություն իմաստ ունի միայն որոշման տիրույթի արժեքների համար:

Եթե կոտորակների հայտարարները հակադիր արտահայտություններ են, ապա դրանց գումարելու կամ հանելու համար պետք է սկզբում կիրառել հանրահաշվական կոտորակների նշանների փոփոխման կանոնը,

ապա գումարել կամ հանել հավասար հայտարարներով կոտորակները:

\frac{3 a}{m - n}

\frac{2 a}{n - m}

կոտորակները գումարելու համար սկզբում փոխում ենք

\frac{2 a}{n - m}

կոտորակի և նրա հայտարարի նշանները, ապա հանում ենք կոտորակների համարիչները՝

\frac{3 a}{m - n} + \frac{2 a}{n - m} = \frac{3 a}{m - n} - \frac{2 a}{- (n - m)} = \frac{3 a}{m - n} - \frac{2 a}{m - n} = \frac{a}{m - n}

\frac{3 y}{y - 5}

\frac{y}{5 - y}

կոտորակները հանելու համար սկզբում փոխում ենք

\frac{y}{5 - y}

կոտորակի և նրա հայտարարի նշանները, ապա գումարում ենք կոտորակների համարիչները՝

\frac{3 y}{y - 5} - \frac{y}{5 - y} = \frac{3 y}{y - 5} + \frac{y}{- (5 - y)} = \frac{3 y}{y - 5} + \frac{y}{- 5 + y} = \frac{3 y}{y - 5} + \frac{y}{y - 5} = \frac{3 y + y}{y - 5} = \frac{4 y}{y - 5}

Օրինակ

Ապացուցենք, որ

F (a) = \frac{2 a^{2} + a}{a^{2} - 7} - \frac{1 + a}{7 - a^{2}} - \frac{15 + 2 a}{a^{2} - 7}

արտահայտության արժեքը կախված չէ փոփոխականի արժեքից:

Լուծում:

Սկզբում ձևափոխենք երկրորդ կոտորակը՝ փոխելով կոտորակի և նրա հայտարարի նշանները՝

- \frac{1 + a}{7 - a^{2}} = \frac{1 + a}{- (7 - a^{2})} = \frac{1 + a}{a^{2} - 7}

Հիմա բոլոր կոտորակների հայտարարները հավասար են, և կարելի է կիրառել նույն հայտարարով կոտորակների գումարման կանոնը՝

\begin{array}{l} F (a) = \frac{2 a^{2} + a}{a^{2} - 7} - \frac{1 + a}{7 - a^{2}} - \frac{15 + 2 a}{a^{2} - 7} = \frac{2 a^{2} + a}{a^{2} - 7} + \frac{1 + a}{a^{2} - 7} - \frac{15 + 2 a}{a^{2} - 7} = \\ \frac{2 a^{2} + a + 1 + a - (15 + 2 a)}{a^{2} - 7} = \frac{2 a^{2} + a + 1 + a - 15 - 2 a}{a^{2} - 7} = \\ = \frac{2 a^{2} - 14}{a^{2} - 7} = \frac{2 (a^{2} - 7)}{a^{2} - 7} = 2 \end{array}

Աղբյուրները

Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շեվկին, Հանրահաշիվ, 8-րդ դասարան, Անտարես, 2012:

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Հանրահաշվական կոտորակների գումարումն ու հանումը

Տեսություն