
















Բուրգի հասկացությունը
Բուրգի մասին դուք նախնական տեղեկություններ ունեք: Հին աշխարհի յոթ հրաշալիքներից են Եգիպտական բուրգերը:

Բուրգերի հաճախ ենք հանդիպում նաև հայկական ճարտարապետական կոթողներում:
Մասնավորապես, եկեղեցիներից շատերի գմբեթներն ունեն բուրգի տեսք:

Բուրգն այն բազմանիստն է, որի նիստերից մեկը բազմանկյուն է, իսկ մյուս բոլոր նիստերն ընդհանուր գագաթով եռանկյուններ են:
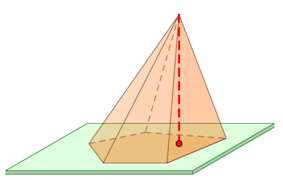
Բազմանկյունը կոչվում է բուրգի հիմք, իսկ նույն գագաթով եռանկյունները՝ կողմնային նիստեր: Բուրգի գագաթից հիմքի հարթությանն իջեցված ուղղահայացը կոչվում է բուրգի բարձրություն:
Եթե բուրգի հիմքը \(n\)-անկյուն բազմանկյուն է, ապա բուրգն անվանում են \(n\)-անկյուն բուրգ:
\(n\)-անկյուն բուրգն ունի \(2n\) կող, որոնցից \(n\)-ը հիմքի կողերն են, իսկ \(n\)-ը՝ կողմնային կողերը:
\(n\)-անկյուն բուրգն ունի \(n+1\) նիստ, որոնցից \(1\)-ը հիմքն է, իսկ \(n\)-ը՝ կողմնային նիստերը:
\(n\)-անկյուն բուրգն ունի \(n+1\) գագաթ, որոնցից \(1\)-ը բուրգի գագաթն է, իսկ \(n\)-ը՝ հիմքի գագաթներն են:
Բուրգի լրիվ մակերևույթը բաղկացած է հիմքից և կողմնային մակերևույթից:
Ուստի բուրգի լրիվ մակերևույթի մակերեսը հավասար է՝ :
Աղբյուրները
Ս. Հակոբյան, Երկրաչափություն 10-րդ դասարան, ՏԻԳՐԱՆ ՄԵԾ, 2009