Եռանկյան և սեղանի մակերեսները — դաս։ Երկրաչափություն, 8-րդ դասարան.

Եռանկյան մակերեսը

Քանի որ զուգահեռագծի անկյունագիծը այն բաժանում է երկու հավասար եռանկյունների, ապա եռանկյան մակերեսը հավասար է զուգահեռագծի մակերեսի կեսին:

S_{եռանկյուն} = \frac{a h_{a}}{2}

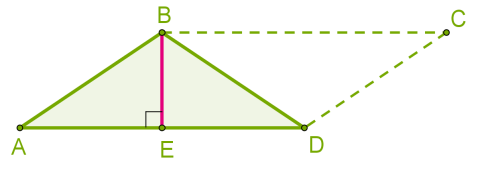
, որտեղ \(h\)-ը ուղղանկյան բարձրությունն է (նկարում՝ \(BE\)-ն), որը տարված է \(a\) կողմին (նկարում՝ \(AD\)-ն):

Եռանկյան մակերեսը հաշվելու համար կարելի է օգտագործել եռանկյան ցանկացած կողմը և նրան տարված բարձրությունը:

Երբեմն, եթե հայտնի են եռանկյան բոլոր երեք կողմերը, հարմար է օգտագործել Հերոնի բանաձևը՝

\begin{array}{l} S_{Δ} = \sqrt{p (p - a) (p - b) (p - c)} \\ p = \frac{a + b + c}{2} \end{array}

որտեղ \(a, b\) և \(c\)-ն եռանկյան կողմերն են, իսկ \(p\)-ն՝ կիսապարագիծը:

Ուղղանկյուն եռանկյան մակերեսը

Քանի որ ուղղանկյուն եռանկյան էջերը փոխուղղահայաց են, ապա մի էջը կարելի է դիտարկել՝ որպես կողմ, իսկ մյուսը՝ որպես բարձրություն, տարված այդ կողմին: Ստանում ենք հետևյալ բանաձևը՝

S = \frac{a \cdot b}{2}

, որտեղ \(a\)-ն և \(b\)-ն էջերն են:

Ուղղանկյուն եռանկյան համար ուժի մեջ է նաև եռանկյան մակերեսի ընդհանուր բանաձևը:

Օրինակ

1. Հաշվենք \(17\) սմ, \(39\) սմ, \(44\) սմ կողմերով եռանկյան մակերեսը:

Լուծում: Կիրառենք Հերոնի բանաձևը.

\begin{array}{l} p = \frac{17 + 39 + 44}{2} = 50 \\ S_{Δ} = \sqrt{50 \cdot (50 - 17) \cdot (50 - 39) \cdot (50 - 44)} = \sqrt{50 \cdot 33 \cdot 11 \cdot 6} = \sqrt{25 \cdot 2 \cdot 3 \cdot 11 \cdot 11 \cdot 2 \cdot 3} = 5 \cdot 2 \cdot 3 \cdot 11 = 330 ({սմ}^{2}) \end{array}

Արմատը հաշվելու հարմար էր ոչ թե բազմապատկել բոլոր արմատատակ թվերը, այլ դրանք վերլուծել արտադրիչների՝

\sqrt{a \cdot a} = a

Հերոնի բանաձևը կարելի է օգտագործել նաև եռանկյան բարձրությունը հաշվելու համար:

Օրինակ

2. Հաշվենք \(15\) սմ, \(13\) սմ, \(4\) սմ կողմերով եռանկյան փոքր բարձրությունը:

Լուծում: Կիրառենք եռանկյան մակերեսի երկու բանաձևեր՝

S_{Δ} = \frac{a h_{a}}{2}

S_{Δ} = \sqrt{p (p - a) (p - b) (p - c)}

Փոքր բարձրությունը տարված է մեծ կողմին, ուրեմն՝ \(a =\)\(15\) սմ:

S_{Δ} = \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{16 \cdot 1 \cdot 3 \cdot 12} = 24 ({սմ}^{2})

Կազմում ենք հավասարումը՝

\begin{array}{l} \frac{15 \cdot h}{2} = 24| \cdot 2 \\ 15 \cdot h = 48 \\ h = \frac{48}{15} = 3,2 (սմ) \end{array}

Երբեմն Հերոնի բանաձևը օգտագործում են զուգահեռագծի մակերեսը հաշվելու համար, եթե հայտնի են զուգահեռագծի կողմերը և անկյունագիծը:

Օրինակ

3. Տրված է \(17\) սմ, \(39\) սմ կողմերով և \(44\) սմ անկյունագծով զուգահեռագիծը: Հաշվենք զուգահեռագծի մակերեսը:

Լուծում:

Անկյունագիծը զուգահեռագիծը բաժանում է երկու հավասար եռանկյունների: Յուրաքանչյուր եռանկյան մակերեսը հաշվելու համար օգտագործենք Հերոնի բանաձևը, ինչպես առաջին օրինակում՝

S_{զուգահեռագիծ} = 2 \cdot S_{Δ} = 2 \cdot 330 = 660 ({սմ}^{2})

Սեղանի մակերեսը

Սեղանի երկու հիմքերը զուգահեռ են, հետևաբար, նրանց միացնող ուղղահայացը սեղանի բարձրությունն է: Սովորաբար բարձրությունը տանում են գագաթից, կամ անկյունագծերի հատման կետով:

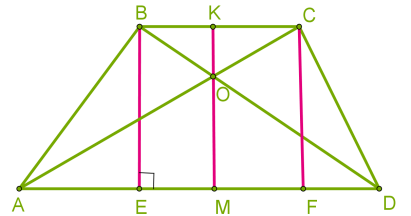
Բարձրությամբ և անկյունագծով սեղանը բաժանվում է երեք եռանկյունների: Սեղանի մակերեսը հաշվում ենք, որպես այդ եռանկյունների մակերեսների գումար:

\begin{array}{l} S_{ABCD} = S_{ABD} + S_{DBC} \\ S_{ABCD} = \frac{AD \cdot BE}{2} + \frac{BC \cdot DF}{2} = \frac{AD \cdot BE}{2} + \frac{BC \cdot BE}{2} = \frac{(AD + BC) \cdot BE}{2} \end{array}

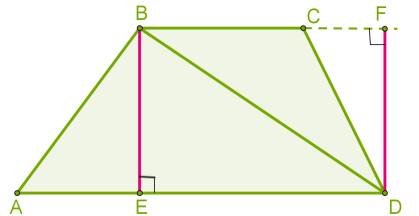
Եթե սեղանի զուգահեռ կողմերը (հիմքերը) նշանակենք \(a\) և \(b\), իսկ բարձրությունը՝ \(h\), ապա՝

S_{սեղան} = \frac{a + b}{2} \cdot h

Ուշադրություն

Նշենք մի քանի կարևոր հետևանքներ:

1. Եթե եռանկյունների բարձրությունները հավասար են, ապա նրանց մակերեսները հարաբերվում են ինչպես հիմքերը:

2. Եթե եռանկյունների հիմքերը հավասար են, ապա նրանց մակերեսները հարաբերվում են ինչպես բարձրությունները:

3. Եթե եռանկյունների բարձրություններն ու հիմքերը հավասար են, ապա եռանկյունները հավասարամեծ են: Օրինակ՝ միջնագիծը եռանկյունը բաժանում է երկու հավասարամեծ եռանկյունների:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցեվ, Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007:

Նախորդ տեսություն

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

2. Եռանկյան և սեղանի մակերեսները

Տեսություն