
















Կանոնավոր բազմանկյուններ
Կանոնավոր կոչվում են այն ուռուցիկ բազմանկյունները, որոնց բոլոր կողմերը և անկյունները հավասար են:
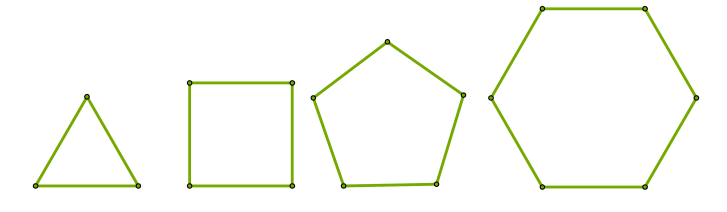
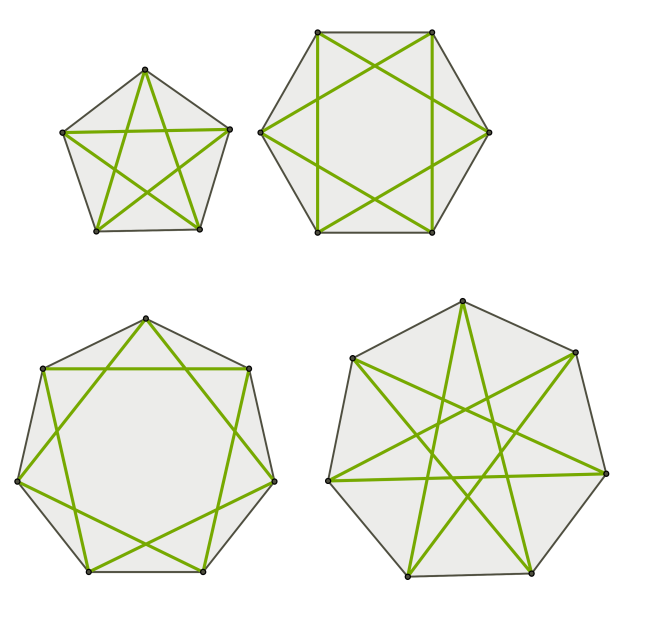
Եթե կանոնավոր բազմանկյան մեջ տանենք անկյունագծեր, ապա կստացվեն կանոնավոր ոչ ուռուցիկ բազմանկյուններ:
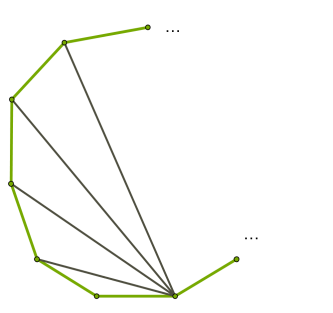
Եթե անկյունագծերը տանենք նույն գագաթից, ապա կանոնավոր \(n\)-անկյունը կբաժանվի \(n-2\) եռանկյունների:
Ուշադրություն
Կանոնավոր \(n\)-անկյան ներքին անկյունների գումարը է:
Քանի որ, կանոնավոր \(n\)-անկյան բոլոր անկյունները հավասար են, ապա դրանցից մեկի աստիճանային չափը կլինի`
Կանոնավոր բազմանկյան ներգծյալ և արտագծյալ շրջանագծերը
Ցանկացած կանոնավոր բազմանկյանը կարելի է ներգծել և արտագծել շրջանագծեր: Երկու շրջանագծերի կենտրոնները համընկնում են և կոչվում են կանոնավոր բազմանկյան կենտրոն:
Ներգծյալ շրջանագիծը շոշափում է բազմանկյան բոլոր կողմերը նրանց միջնակետերում, արտագծյալ շրջանագիծը անցնում է բազմանկյան բոլոր գագաթներով:
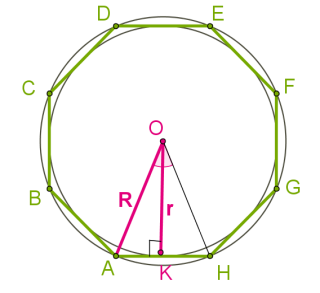
Հավասարակողմ եռանկյան (կանոնավոր եռանկյուն) և քառակուսու (կանոնավոր քառանկյուն) համար մեր դիտարկած բանաձևերը մնում են ուժի մեջ:
Աղբյուրները
Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև Է.Գ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 8-րդ դասարան, Երևան, "Զանգակ 97", 2007: