Կոսինուսների թեորեմը — դաս։ Երկրաչափություն, 9-րդ դասարան.

Կոսինուսների թեորեմը

Ուղղանկյուն եռանկյան մեջ տարրերի որոշման համար բավական է իմանալ եռանկյան որևէ երկու տարրեր (երկու կողմ, կողմ ու անկյուն):

Կամայական եռանկյան դեպքում պետք է իմանալ գոնե \(3\) տարր:

Կոսինուսների թեորեմը

Եռանկյան կողմի քառակուսին հավասար է մյուս երկու կողմերի քառակուսիների գումարին՝ հանած այդ կողմերի և դրանց կազմած անկյան կոսինուսի արտադրյալի կրկնապատիկը:

a^{2} = b^{2} + c^{2} - 2 \cdot b \cdot c \cdot cosA

Եռանկյունը տեղադրենք կոորդինատային հարթության մեջ այնպես, որ \(A\) գագաթը համընկնի սկզբնակետի հետ, իսկ \(B\) գագաթը գտնվի աբսցիսների առանցքի վրա (տես նկարը):

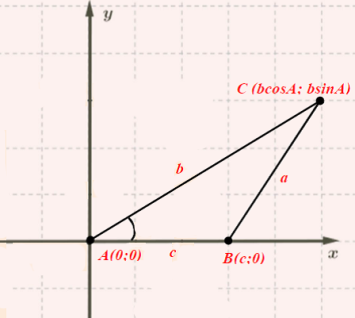
\(C\) գագաթը կունենա \(C (b·cosA; b·sinA)\) կոորդինատները:

Ըստ երկու կետերի հեռավորության բանաձևի հաշվենք \(BC\) հատվածի երկարությունը՝

\begin{array}{l} {a^{2} = BC}^{2} = {(b \cdot cosA - c)}^{2} + b^{2} \sin^{2} A = \\ = b^{2} \cos^{2} A - 2 bc \cdot cosA + c^{2} + b^{2} \sin^{2} A = \\ = b^{2} (\cos^{2} A + \sin^{2} A) + c^{2} - 2 bc \cdot cosA = \\ = b^{2} + c^{2} - 2 bc \cdot cosA \end{array}

Ապացուցված բանաձևը ճիշտ է եռանկյան ցանկացած կողմի համար՝

b^{2} = a^{2} + c^{2} - 2 \cdot a \cdot c \cdot cosB

c^{2} = a^{2} + b^{2} - 2 \cdot a \cdot b \cdot cosC

Կոսինուսների թեորեմը կիրառում են՝

եռանկյան անհայտ կողմը գտնելու համար, եթե տրված են մյուս երկու կողմերը և նրանց կազմած անկյունը,
անկյան կոսինուսը գտնելու համար, եթե տրված են եռանկյան բոլոր կողմերը:

Կոսինուսների թեորեմը անվանում են նաև Պյութագորասի ընդհանրացված թեորեմ, քանի որ, եթե \(A\)-ն ուղիղ անկյուն է (հետևաբար, \(cosA = 0\)), ապա ստանում ենք Պյութագորասի թեորեմը:

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, «Զանգակ», 2013

Վերադառնալ թեմային

Հաջորդ առաջադրանքը

Գրեք մեզ

Սխա՞լ ես գտել

Տեղեկացրու մեզ

1. Կոսինուսների թեորեմը

Տեսություն