Հեռավորությունը երկու կետերի միջև — դաս։ Երկրաչափություն, 9-րդ դասարան.

Հեռավորությունը կետերի միջև

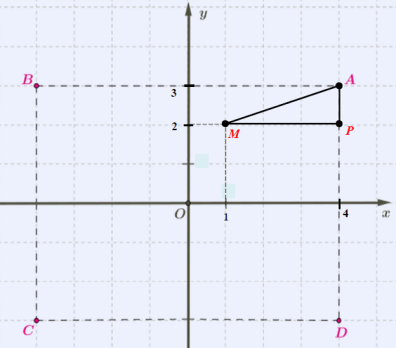
Հաշվենք

MA

հեռավորությունը

M (1; 2)

A (4; 3)

կետերի միջև:

Այդ կետերից տանենք կոորդինատային առանցքներին զուգահեռ հատվածներ և դիտարկենք առաջացած

APM

ուղղանկյուն եռանկյունը:

Հաշվենք

APM

եռանկյան

MP

AP

էջերը՝

MP = 4 - 1 = 3, AP = 3 - 2 = 1

Ունենալով

APM

ուղղանկյուն եռանկյան էջերը, Պյութագորասի թեորեմի միջոցով, գտնում ենք եռանկյան

MA

ներքնաձիգը՝

MA = \sqrt{{MP}^{2} + {AP}^{2}} = \sqrt{3^{2} + 1^{2}} = \sqrt{10}

Այս օրինաչափությունը տեղի ունի նաև ընդհանուր դեպքում:

Եթե կոորդինատային հարթության վրա տրված են երկու կետեր՝

K (x_{0}; y_{0})

L (x_{1}; y_{1})

, ապա այդ կետերի միջև

d_{KL}

հեռավորությունը կարելի է հաշվել հետևյալ բանաձևով՝

d_{KL} = \sqrt{{(x_{1} - x_{0})}^{2} + {(y_{1} - y_{0})}^{2}}

Այսպիսով, հարթության վրա տրված երկու կետերը միացնող հատվածի երկարությունը հավասար է՝

d_{KL} = \sqrt{{(x_{1} - x_{0})}^{2} + {(y_{1} - y_{0})}^{2}}

Աղբյուրները

Լ.Ս. Աթանասյան, Վ.Ֆ. Բուտուզով, Ս.Բ. Կադոմցև, Է.Հ. Պոզնյակ, Ի.Ի..Յուդինա: Երկրաչափություն 9-րդ դասարան, Երևան, Զանգակ, 2013

Սխա՞լ ես գտել

2. Հեռավորությունը երկու կետերի միջև