
















Թվային ֆունկցիա, նրա որոշման տիրույթն ու արժեքների բազմությունը
Ֆունկցիայի գաղափարին արդեն ծանոթ ենք \(7\)-րդ դասարանի հանրահաշվի դասընթացից:
Հիշենք այդ սահմանումը:
Դիցուք \(X\)-ը որևէ թվային բազմություն է: Եթե այդ բազմության յուրաքանչյուր \(x\) թվի որոշակի \(f\) օրենքով համապատասխանության մեջ է դրվում ճիշտ մեկ \(y\) թիվ, ապա ասում են, որ \(X\) բազմության վրա տրված է \(y = f(x)\) ֆունկցիան:
\(X\) բազմությունը անվանում են \(y = f(x)\) ֆունկցիայի որոշման տիրույթ:
\(x\)-ը անվանում են անկախ փոփոխական կամ արգումենտ, իսկ նրան համապատասխանող \(y\) թիվը՝ կախյալ փոփոխական կամ ֆունկցիայի արժեք \(x\) կետում: \(f(x)\) ֆունկցիայի բոլոր արժեքների բազմությունն անվանում են \(y = f(x)\) ֆունկցիայի արժեքների բազմություն:
\(f \) ֆունկցիայի որոշման տիրույթը ընդունված է նշանակել \(D(f)\)-ով, իսկ արժեքների տիրույթը՝ \(E(f)\)-ով:
Սահմանումից հետևում է, որ ֆունկցիայի տրման համար պետք է նկարագրված լինի \(f \) կանոնը` իր որոշման տիրույթի հետ միասին: Սակայն հաճախ, երբ ֆունկցիան տրված է լինում անալիտիկ՝ բանաձևով, որոշման տիրույթը բացահայտ չի նշվում:
Այդ դեպքերում ֆունկցիայի որոշման տիրույթը անկախ փոփոխականի բոլոր այն արժեքների բազմությունն է, որոնցից յուրաքանչյուրի համար ֆունկցիան ընդունում է իրական արժեքներ:
Վերհիշենք նաև, որ ֆունկցիայի գրաֆիկ անվանում են \(xOy\) կոորդինատային հարթության վրա տեսքի բոլոր կետերի բազմությունը, որտեղ \(x\)-ը որոշման տիրույթի կամայական կետ է:
Ֆունկցիայի արժեքների բազմությունը գտնելու խնդիրը ընդհանուր դեպքում բարդ է:
Այդ խնդիրը լուծելու համար հարմար է կառուցել ֆունկցիայի գրաֆիկը և տեսնել, թե ի՞նչ բազմություն է իրենից ներկայացնում գրաֆիկի պրոյեկցիան օրդինատների առանցքի վրա:
Օրինակ
Դիցուք ֆունկցիայի գրաֆիկն ունի հետևյալ տեսքը՝
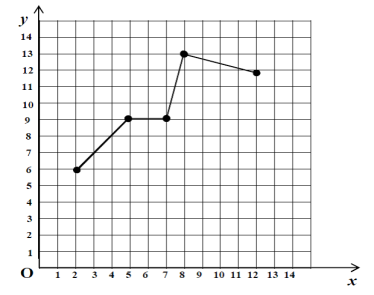
Տեսնում ենք, որ այս ֆունկցիայի գրաֆիկի պրոյեկցիան օրդինատների առանցքի վրա հատվածն է: Ուստի՝
Եթե դիտարկեինք տրված ֆունկցիայի գրաֆիկի պրոյեկցիան աբսցիսների առանցքի վրա, ապա կստանայինք նրա որոշման տիրույթը՝
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013