
















Երկու անհայտներով երկու հավասարումների համակարգի գրաֆիկական եղանակով լուծման ալգորիթմը:
1. Կառուցել առաջին հավասարման գրաֆիկը:
2. Կառուցել երկրորդ հավասարման գրաֆիկը:
3. Գտնել երկու գրաֆիկների հատման կետերը:
4. Որպես պատասխան գրել բոլոր \((x; y)\) հատման կետերը:
Օրինակ
Լուծենք համակարգը:
Լուծում:
1. Կառուցենք հավասարման գրաֆիկը:
Գրաֆիկը \(3\) շառավիղով շրջանագիծ է, որի կենտրոնը կոորդինատների սկզբնակետն է:
2. հավասարման մեջ արտահայտենք \(y\)-ը և կառուցենք հավասարման գրաֆիկը:
Գրաֆիկն ուղիղ գիծ է, որն անցնում է \((0; -3)\) և \((3; 0)\) կետերով:
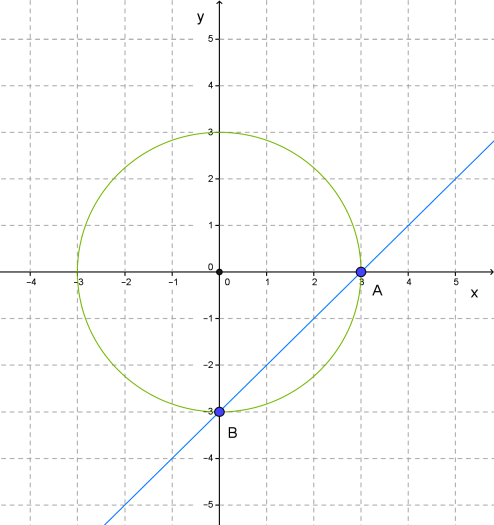
3. Շրջանագիծը և ուղիղը հատվում են \(A\) և \(B\) կետերում:
\(A\) կետի կոորդինատներն են՝ \((3; 0)\), \(B\) կետի կոորդինատները՝ \((0; -3)\)
\((3; 0)\) և \((0; -3)\) կետերը լուծումներ են համակարգի միաժամանակ երկու հավասարումների, ուրեմն նաև՝ համակարգի համար:
Պատասխան՝ \((3; 0)\) և \((0; -3)\)
Աղբյուրները
Ս. Մ. Նիկոլսկի, Մ.Կ. Պոտապով, Ն.Ն. Րեշետնիկով, Ա.Վ. Շևկին, Հանրահաշիվ, 9-րդ դասարան, Անտարես, 2013